Предмет: Алгебра,
автор: vadimbabyshin586
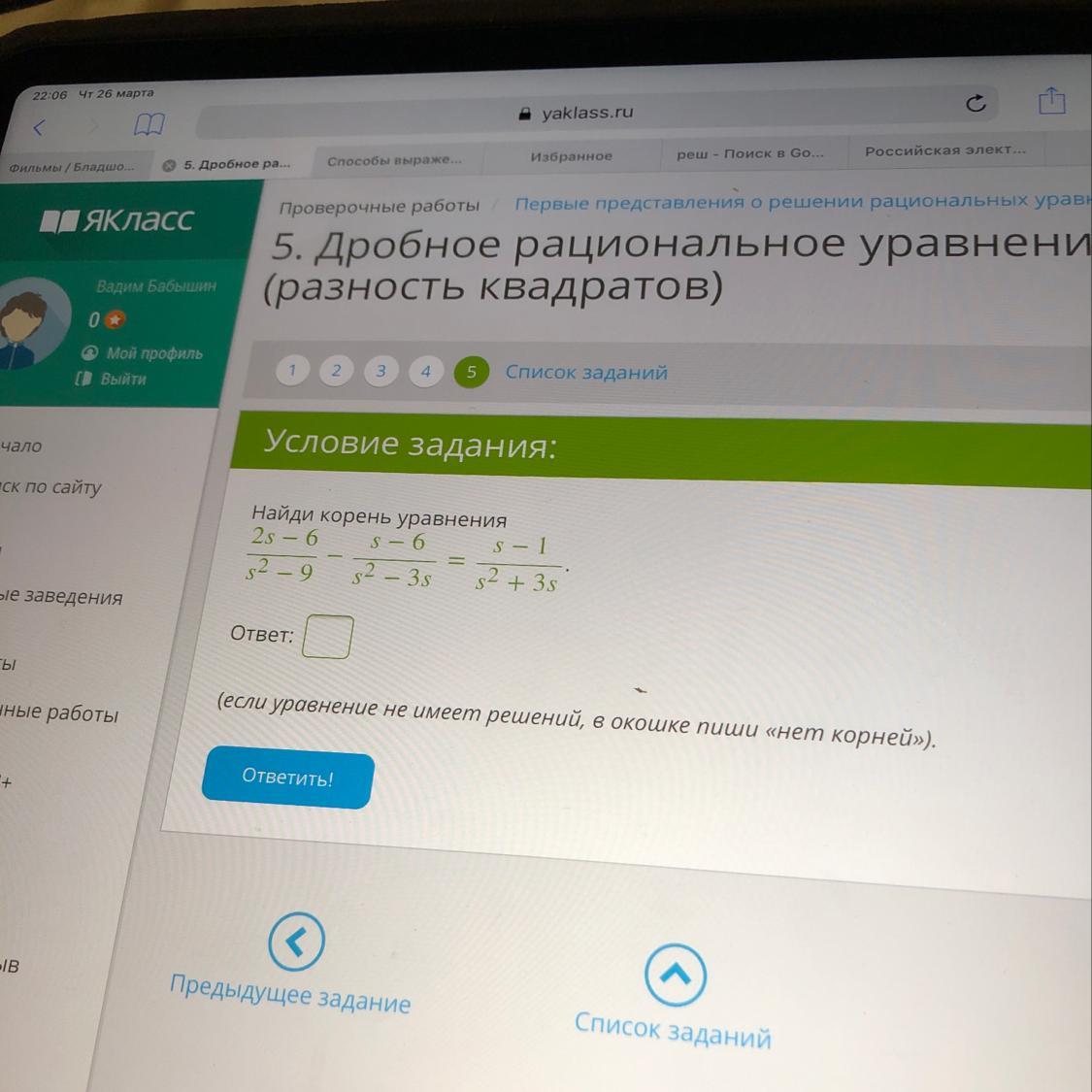
Найди корень уравнения
Приложения:
vadimbabyshin586:
Не надо
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: dasha17064
Предмет: Русский язык,
автор: valeavalea
Предмет: Английский язык,
автор: Kamulik
Предмет: Литература,
автор: кешаслшп
Предмет: Алгебра,
автор: kqyuantt