Question

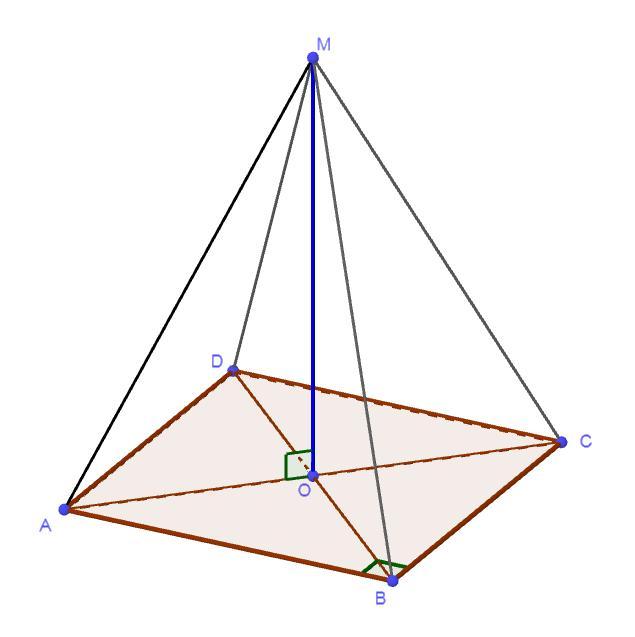
Через точку О пересечения диагоналей квадрата со стороной 4 см проведена прямая OM перпендикулярная плоскости квадрата. Найдите расстояние от точки М до вершин квадрата, если ОМ= 5 см

Заранее спасибо! (50 баллов!!)

Answer 1

Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.

Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк$d^2=a^2+a^2\\d=\sqrt{a^2+a^2} \\AC=\sqrt{4^2+4^2}=\sqrt{16+16}=\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2} \:\: (cm)$а пересечения делит их пополам.

Р-м ΔAOM:

∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.

AO = d/2

Ищем, чему равна диагональ квадрата:

$d^2=a^2+a^2\\d=\sqrt{a^2+a^2} \\d=\sqrt{4^2+4^2}=\sqrt{16+16} =\sqrt{32}= 4\sqrt{2} \:\:(cm)$

AO = (4√2)/2 = 2√2 см

Теперь можем найти длину отрезка AM

$AM=\sqrt{AO^2+OM^2} \\AM=\sqrt{(2\sqrt{2})^2+5^2}=\sqrt{4\cdot 2+25} =\sqrt{33} \approx 5.74 \:\: (cm)$

Ответ: Расстояние равно √33 см, или приблизительно 5,74 см.