Предмет: Алгебра,
автор: YanaK
алгебра, вычисление интегралов
Приложения:
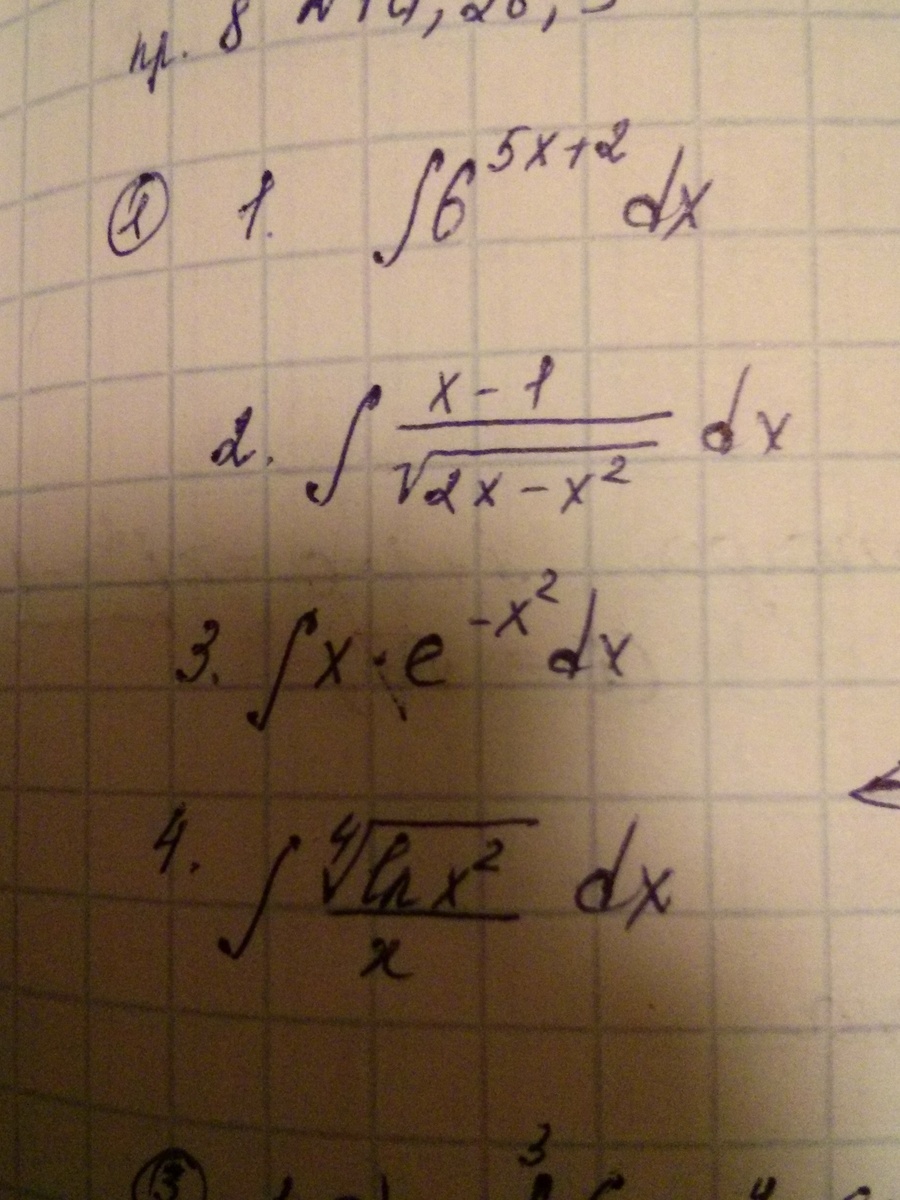
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: arsenshamil91
Предмет: Математика,
автор: danksal39
Предмет: Алгебра,
автор: nkamilb
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: Лена135