CA = 72 см;
CB = 30 см.
AB =
см;
(дроби сокращай).
sin∢B=
;
cos∢B=
.
Ответы
Ответ:
Объяснение:
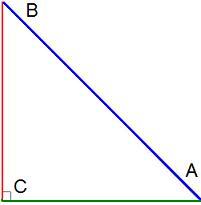
Посмотрим на данный прямоугольный треугольник:
На рисунке ∡С помечен как прямоугольный, значит СА и СВ - катеты треугольника, а АВ - гипотенуза. СА = 72 см, СВ = 30 см.
∡В - острый, а ∆АВС - прямоугольный.
Чтобы найти синус острого угла прямоугольного треугольника нужно поделить длину противолежащего катета на длину гипотенузы.
Чтобы найти косинус острого угла прямоугольного треугольника нужно поделить длину прилежащего катета на длину гипотенузы.
Найдём гипотенузу этого треугольника, используя т. Пифагора:
c² = a²+b² => c = √(a²+b²)
В данном случае:
AB = √(СА²+СВ²) = √(72²+30²) = √(5184+900) = √6084 = 78 см.
Для ∡В противолежащий катет - это СА, а АВ - гипотеза. Зная это, найдём синус ∡В:
sin ∡В = CA/АВ = 72/78 = 12/13.
Для ∡В прилежащий катет - это СВ, а АВ - гипотеза. Зная это, найдём косинус ∡В:
cos ∡В = СВ/АВ = 30/78 = 5/13.