Предмет: Математика,
автор: Ma28sha
ПОМОГИТЕ!!!(
Кто-нибудь знает высшую математику??
Тема: исследование функции
Пример на фотке
Приложения:
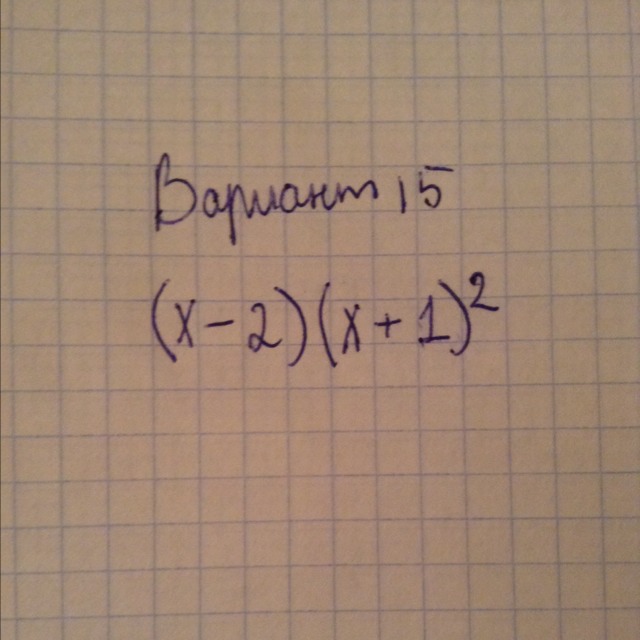
Ответы
Автор ответа:
0
1)D(f) = R
Область значений можно не находить, если это слишком сложно, как здесь, я и не буду этим заморачиваться.
2)Определим, чётна ли функция, или же нечётна, или же не является ни той, ни другой. Для удобства сначала раскрою скобки:
(x-2)(x^2 + 2x + 1) = x^3 + 2x^2 + x - 2x^2 - 4x - 2 = x^3 - 3x - 2
f(-x) = (-x)^3 - 3(-x) - 2 = -x^3 + 3x - 2 - не является ни чётной, ни нечётной.
3)Исследуем функцию на монотонность и экстремумы:
1)Вычислим производную:
y' = 3x^2 - 3
D(y') = R, производная всюду существует, функция не имеет критических точек первого рода.
2)Найдём стационарные точки:
y' = 0
3x^2 - 3 = 0
x^2 - 1 = 0
(x-1)(x+1) = 0
x = -1 или x = 1
Исходная функция возрастает на интервале (-беск;-1) и (1;+беск), так как производная на этих интервалах положительна.
Функция убывает на (-1;1), здесь производная отрицательна.
4)Функция имеет точку максимума x(max) = -1 и точку минимума x(min) = 1
5)Нули и промежутки знакопостоянства пропустим в данном случае, поскольку в этом случае придётся решать уравнение x^3 - 3x - 2 = 0, что довольно проблематично.
6)Исследуем наконец нашу функцию на наличие асимптот.
Горизонтальной асимптоты функция не имеет, поскольку не существует предела
lim(x-> беск) (x^3 - 3x - 2), а точнее, он равен бесконечности.
Тем более не имеет она и вертикальной асимптоты, поскольку функция определена во всех точках.
Область значений можно не находить, если это слишком сложно, как здесь, я и не буду этим заморачиваться.
2)Определим, чётна ли функция, или же нечётна, или же не является ни той, ни другой. Для удобства сначала раскрою скобки:
(x-2)(x^2 + 2x + 1) = x^3 + 2x^2 + x - 2x^2 - 4x - 2 = x^3 - 3x - 2
f(-x) = (-x)^3 - 3(-x) - 2 = -x^3 + 3x - 2 - не является ни чётной, ни нечётной.
3)Исследуем функцию на монотонность и экстремумы:
1)Вычислим производную:
y' = 3x^2 - 3
D(y') = R, производная всюду существует, функция не имеет критических точек первого рода.
2)Найдём стационарные точки:
y' = 0
3x^2 - 3 = 0
x^2 - 1 = 0
(x-1)(x+1) = 0
x = -1 или x = 1
Исходная функция возрастает на интервале (-беск;-1) и (1;+беск), так как производная на этих интервалах положительна.
Функция убывает на (-1;1), здесь производная отрицательна.
4)Функция имеет точку максимума x(max) = -1 и точку минимума x(min) = 1
5)Нули и промежутки знакопостоянства пропустим в данном случае, поскольку в этом случае придётся решать уравнение x^3 - 3x - 2 = 0, что довольно проблематично.
6)Исследуем наконец нашу функцию на наличие асимптот.
Горизонтальной асимптоты функция не имеет, поскольку не существует предела
lim(x-> беск) (x^3 - 3x - 2), а точнее, он равен бесконечности.
Тем более не имеет она и вертикальной асимптоты, поскольку функция определена во всех точках.
Похожие вопросы
Предмет: Химия,
автор: xzzcxxa
Предмет: Қазақ тiлi,
автор: ajbekzumabaev6
Предмет: Қазақ тiлi,
автор: leonidkuzubo45
Предмет: Химия,
автор: AyNur06
Предмет: Алгебра,
автор: Лена135