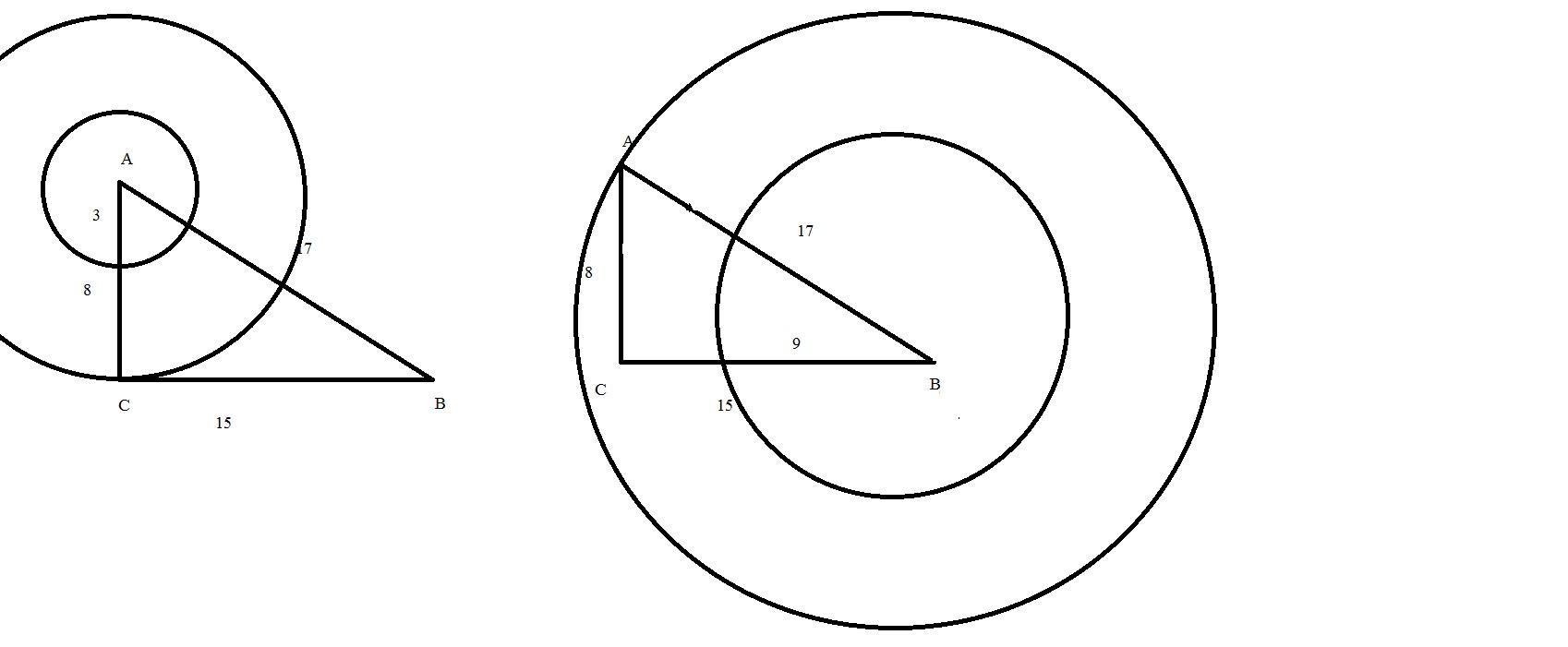
Дан прямоугольный треугольник АВС с прямым углом С, в котором известны стороны АС = 8 см,
ВС = 15 см, АВ = 17 см.
Выберите верные утверждения:
Окружность с центром в точке А и радиусом 3 см имеет с прямой BС две общие точки.
Окружность с центром в точке А и радиусом 8 см имеет с прямой ВС одну общую точку.
Окружность с центром в точке В и радиусом 17 см имеет с прямой АС две общие точки.
Окружность с центром в точке В и радиусом 9 см имеет с прямой AС одну общую точку.
Ответы
Окружность с центром в точке А и радиусом 3 см имеет с прямой BС две общие точки. Не верно.
Поскольку прямая расстояние от центра окружности А до стороны ВС, больше радиуса окружности r<AC, r<AB, то прямая и окружность не имеют общих точек.
Окружность с центром в точке А и радиусом 8 см имеет с прямой ВС одну общую точку. Верно.
Если расстояние от центра окружности до прямой равно ее радиусу, то прямая и окружность имеют одну общую точку касания.
Окружность с центром в точке В и радиусом 17 см имеет с прямой АС две общие точки. Не верно
Поскольку радиус окружность равен гипотенузе r=AB, то А∈окружности. Остальные точки АС не имеют с окружностью общих точек, поскольку меньше радиуса окружности.
Окружность с центром в точке В и радиусом 9 см имеет с прямой AС одну общую точку. НЕ ВЕРНО
Поскольку расстояние от точки В до АС от 15 см до 17 см, то окружность с АС не имеет общих точек.
В приложении есть рисунки для демонстрации утверждений.