Предмет: Алгебра,
автор: zra7s
Решите срочно уравнение 5)
Приложения:
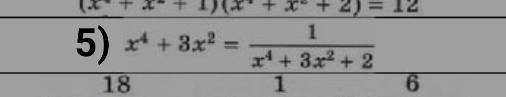
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: dan1234l
Предмет: Английский язык,
автор: трость
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: bestaev06
Предмет: Математика,
автор: ВеликийМагистр131