Предмет: Математика,
автор: repvbx1999
Интегралы
Пожалуйста напишите помимо решения примененную формулу или способ
Приложения:
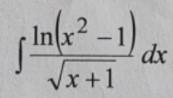
Ответы
Автор ответа:
1
Рассмотрите предложенное решение; оформление не соблюдалось.
В квадратных скобках показаны метод и замена; решение второго интеграла вынесено в отдельный блок и отмечено красным *.
Ответ записан красным.
Основной способ - интегрирование по частям (первые квадратные скобки).
Приложения:

Sholniknapat:
Помогите мне пожалуйста с математикой пожалуйста умоляю
Автор ответа:
0
По свойству логарифмов переписывает логарифм через сумму, далее используем замены.
Похожие вопросы
Предмет: Русский язык,
автор: Angelok4
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Heppik
Предмет: Литература,
автор: aevbryansk
Предмет: Алгебра,
автор: валерия8396