Question

ГЕОМЕТРИЯ !!20 баллов!!
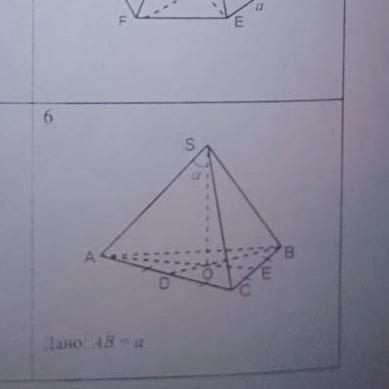
Правильная пирамида. SO - высота правильной пирамиды. Найти площадь полной поверхности пирамиды.

Answer 1

Ответ:

2*a^2*sqrt(3)/(12*cos(alpha)+  sqrt(3)/4*a^2  +sqrt((sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2)*((sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2)-sqrt(3a^2/(36*tg^2(alpha)) +4/3*a^2))^2*(sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2-a)

Объяснение:

ABC - равносторонний треугольник

BD = sqrt((2a^2+2a^2-a^2)/4) = sqrt((3/4)a^2) = sqrt(3)a/2

OD = sqrt(3)a/6 (теорема о пересечении медиан)

AO = 2*sqrt(3)a/3 (та же теорема)

SD=OD/cos(alpha) = sqrt(3)a/(6*cos(alpha))

OS = OD/tg(alpha) = sqrt(3)a/(6*tg(alpha))

S(ASC)=a^2*sqrt(3)/(12*cos(alpha)

Треугольник SOD равен тр-ку SOE (OD=OE - 1/3 медианы, а медиана в правильн. тр-ке одинакова), отсюда SD=SE, а по условию AC=CD, отсюда S(ASC)=S(SCB).

sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)

S(ABC)=sqrt(3)/4*a^2 (площадь правильного тр-ка через сторону)

SA^2 = OS^2+AO^2 =  3a^2/(36*tg^2(alpha)) + 4/3*a^2 (т. Пифа)

SA = sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)

SA=SB, т.к тр-ки ASO и BSO равны (AO=OB - две трети медианы, а медианы равны, SO - общая)

Полуперим тр-ка ASB:2SA+AB=sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2

По формуле герона:

S(ASB)= sqrt((sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2)*((sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2)-sqrt(3a^2/(36*tg^2(alpha)) +4/3*a^2))^2*(sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2-a)

Итог:

S(общ)=  S(ASC) + S(SCB) + S(ABC) + S(ASB) = 2S(ASC)+S(ABC)+S(ASB) =

= 2*a^2*sqrt(3)/(12*cos(alpha)+  sqrt(3)/4*a^2  +sqrt((sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2)*((sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2)-sqrt(3a^2/(36*tg^2(alpha)) +4/3*a^2))^2*(sqrt(3a^2/(36*tg^2(alpha)) + 4/3*a^2)+a/2-a)