Question

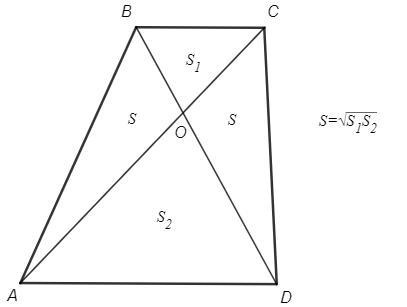
В трапеции ABCD основания AD и BC, диагонали пересекаются в точке О. Площадь ВОС = 12см², площадь AOD = 48см². Найдите площадь трапеции.

Answer 1

S(ABD)=S(ACD) (общее основание, равные высоты)

S(ABD)-S(AOD) =S(ACD)-S(AOD) => S(AOB)=S(COD)

Площади треугольников с равными высотами относятся как их основания.

S(AOB)/S(AOD) =OB/OD =S(BOC)/S(COD) =>

S(AOB)*S(COD) =S(BOC)*S(AOD) =>

S(AOB) =S(COD) =√[S(BOC)*S(AOD)]

S(AOB) = √(12*48) =24 (см^2)

S(ABCD) =12 +48 +2*24 =108 (см^2)