5.3 и 5.5 плз 70б
Это на каникулы

Ответы
Задача 5.3:
BE, CF и AX — высоты треугольника ABC. AX = BE, CX = CCF, AC = 17. Найти длину отрезка BC.
Решение:
Р-м ΔACX и ΔBCE:
Треугольники ACX и BCE — прямоугольные, ∠X = ∠E = 90°
∠ACX = ∠BOE — как вертикальные, AX = BE и CX = EX — по условию.
Треугольники равны по первому признаку равенства треугольников (два катетам и угол между ними), или по второму (катет и прилегающие к нему углы).
Если треугольники равны, равны и их соответствующие элементы:
ΔACX = ΔBCE ⇒ AC = BC, CX = CE, XA = EA, и то же самое с градусными мерами углов.
Следовательно, BC = AC = 17 дм.
Ответ:
Длина отрезка АС равна 17 дм.
Задача 5.5:
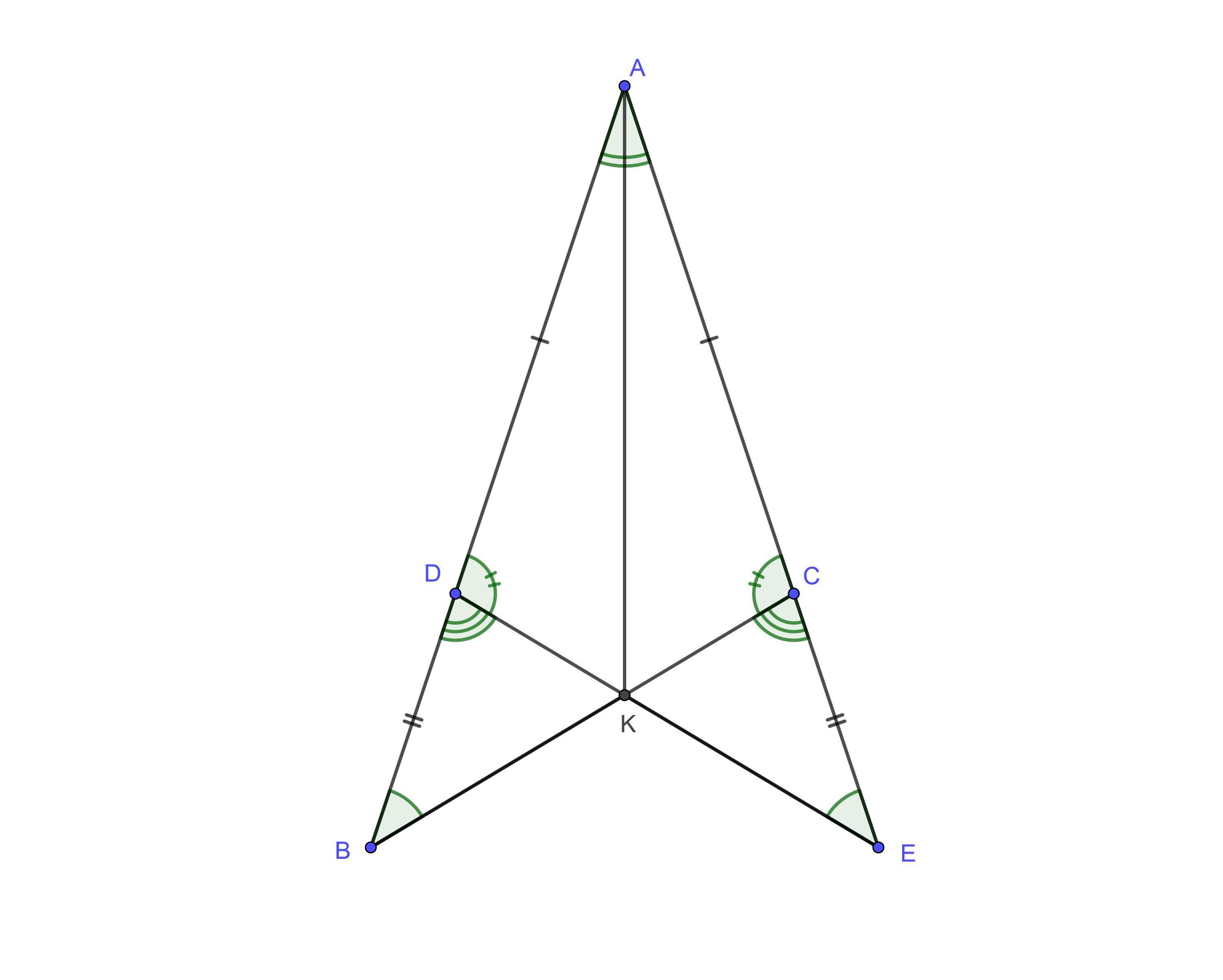
1) На одной стороне угла с вершиной A отмечены точки D и B, на другой стороне — C и E так, что AD = AC = 3 см, AB = AE = 4 см. Доказать, что: а) ВС = DE б) KB = KE, где К — точка пересечения отрезков BC и ED.
Доказательство:
a) Р-м ΔABC и ΔAED:
∠A — общий, AB = AE = 4 см, АС = AD = 3 см — всё дано по условию задачи.
Треугольники ABC и AED равны по первому признаку равенства треугольников (две стороны и угл между ними). Если треугольники равны, равны и соответствующие элементы.
AB = AE, BC = ED, CA = DA ⇒ BC = ED
б)
Т.к. ΔABE = ΔAED, ∠ADE = ∠ACB ⇒ ∠KDB = ∠KCE ⇒ ΔBKD = ΔEKC по второму признаку равенства треугольников (сторона и два прилежащих угла) ⇒ KB = KE.
2) ΔABC и ΔA₁B₁C₁ — равнобедренные треугольники с основаниями AC и A₁C₁ точки К и К₁ — середины сторон BC и B₁C₁ соответственно. AB = A₁B₁, AK = A₁K₁. Доказать, что треугольник ΔABC = ΔA₁B₁C₁.
Доказательство:
Т.к. треугольники ABC и A₁B₁C₁ равнобедренные, то AB = BC, A₁B₁ = B₁C₁ ⇒ BC = B₁C₁.
Т.к. AK, A₁K₁ — медианы, BK=B₁K₁ и KC = K₁C₁.
Р-м ΔABK и ΔA₁B₁K₁:
AB = A₁B₁, BK = B₁K₁, AK = A₁K₁ ⇒ ΔABK и ΔA₁B₁K₁ равны по третьему признаку (три стороны). ⇒ ∠A = ∠A₁.
ΔABC=ΔA₁B₁C₁ по первому признаку равенства треугольников (две стороны и угл).