Предмет: Алгебра,
автор: pranovadiletqwe
Помогите срочно и пожалуйста вычислить интеграл!!!
Приложения:
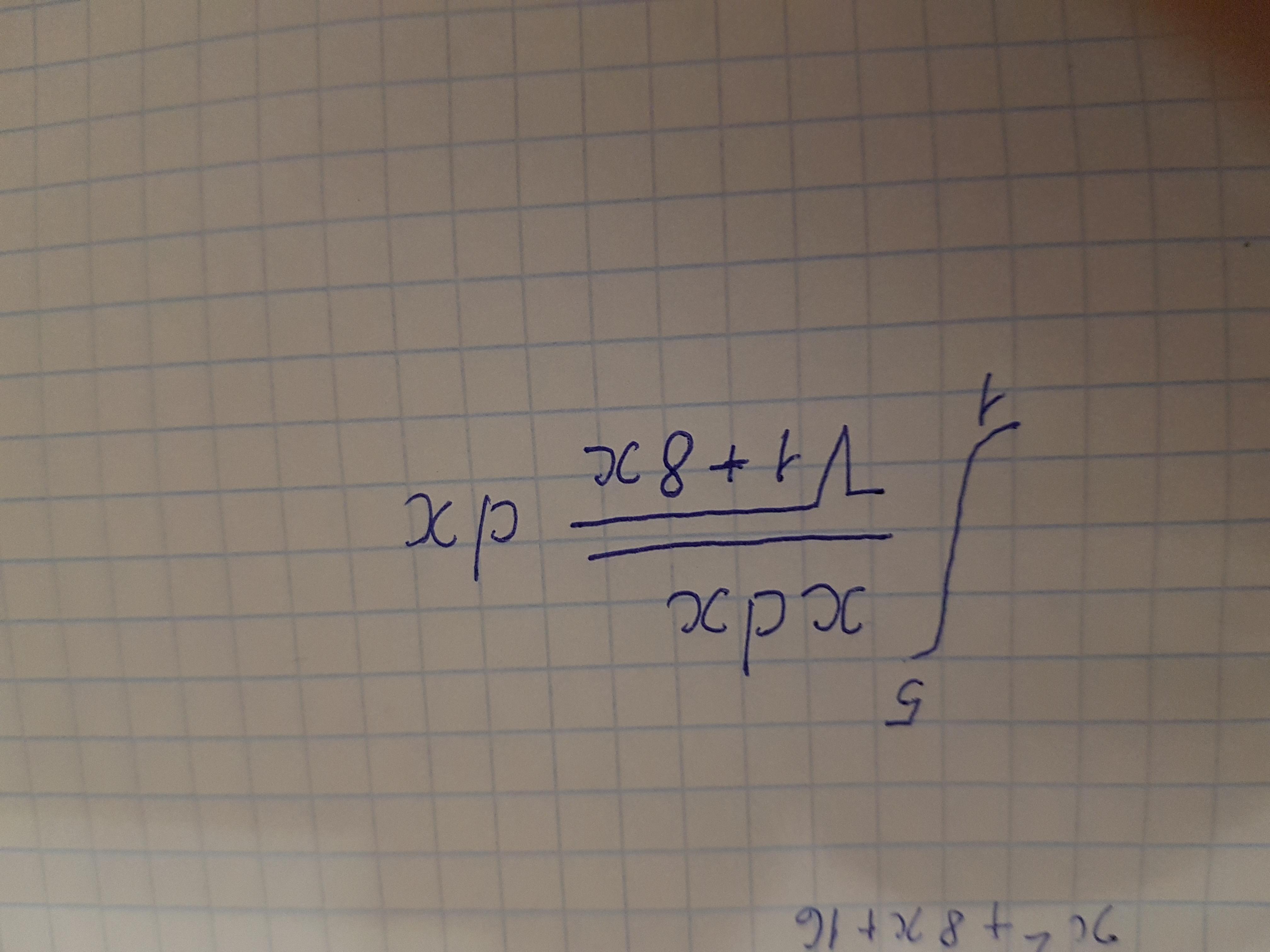
Ответы
Автор ответа:
1
можно применить метод замены переменной:
Пределы интегрирования
при x=1; t=3
при х=5; t=√41
Похожие вопросы
Предмет: Русский язык,
автор: НасТюша2000вил
Предмет: Английский язык,
автор: VickyNayaLovers
Предмет: Русский язык,
автор: 201181
Предмет: Алгебра,
автор: Alka212002
Предмет: Алгебра,
автор: Dauptupoy