Предмет: Математика,
автор: PAIN1999
Найдите общие решения уравнений
Приложения:
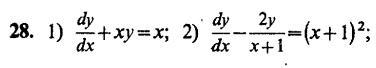
Ответы
Автор ответа:
0
______________________________
Похожие вопросы
Предмет: Русский язык,
автор: Matt174
Предмет: Русский язык,
автор: iren2605
Предмет: Русский язык,
автор: Олюньчик30
Предмет: Математика,
автор: Настя30