Предмет: Алгебра,
автор: berlizovakysa
Доказать Тождество (номер 3)
Приложения:
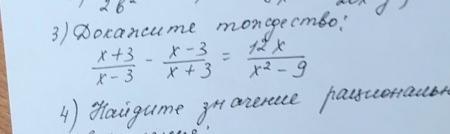
Ответы
Автор ответа:
0
Тождество доказано
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Українська мова,
автор: жека2000003
Предмет: Українська мова,
автор: kurchenko73
Предмет: Русский язык,
автор: евалатыш
Предмет: Математика,
автор: дана196
Предмет: Физика,
автор: Tong69