Решить задачи по геометрии. Параллельные прямые.
Задания на листочке.
100 баллов.
Ответы
Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180°.
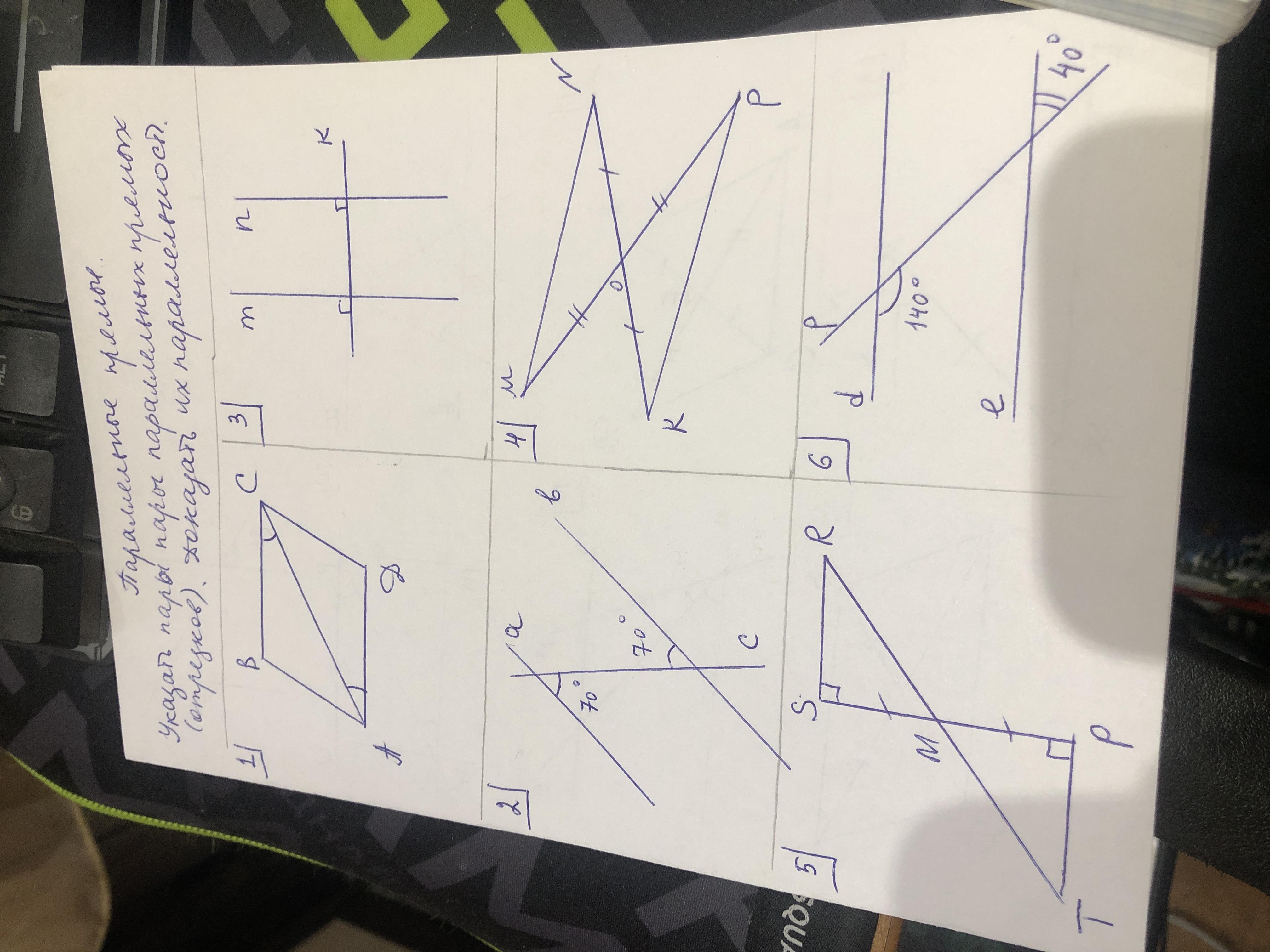
1) BC || AD
∠BCA = ∠CAD — накрест лежащие
2) a || b
накрест лежащие углы равны, сумма односторонних равна 180°
3) m || n
m и n ⊥ k — они уже являются параллельными, но, к дополнению, равны и соответственные углы и сумма односторонних 180°, т.к. все углы по 90°.
4) MN || KP
∠NOM = ∠KOP как вертикальные ⇒ ΔMNO равен ΔPKO по первому признаку равенства треугольников (две стороны и угол между ними)
Пары углов (∠N = ∠K) и (∠M = ∠P) — как накрест лежащие
5) SR || PT
SR и PT ⊥ SP — они уже являются параллельными, но, к дополнению, ∠S = ∠P = 90°, ∠SMR = ∠PMR как вертикальные ⇒ ΔSRM равен ΔPTM по второму признаку равенства треугольников (сторона и два прилегающих угла) .
∠R = ∠T — как накрест лежащие
6) d || e
равны соответствующие углы (по 40° и 140°), и сумма односторонних равна 180° (140+40).
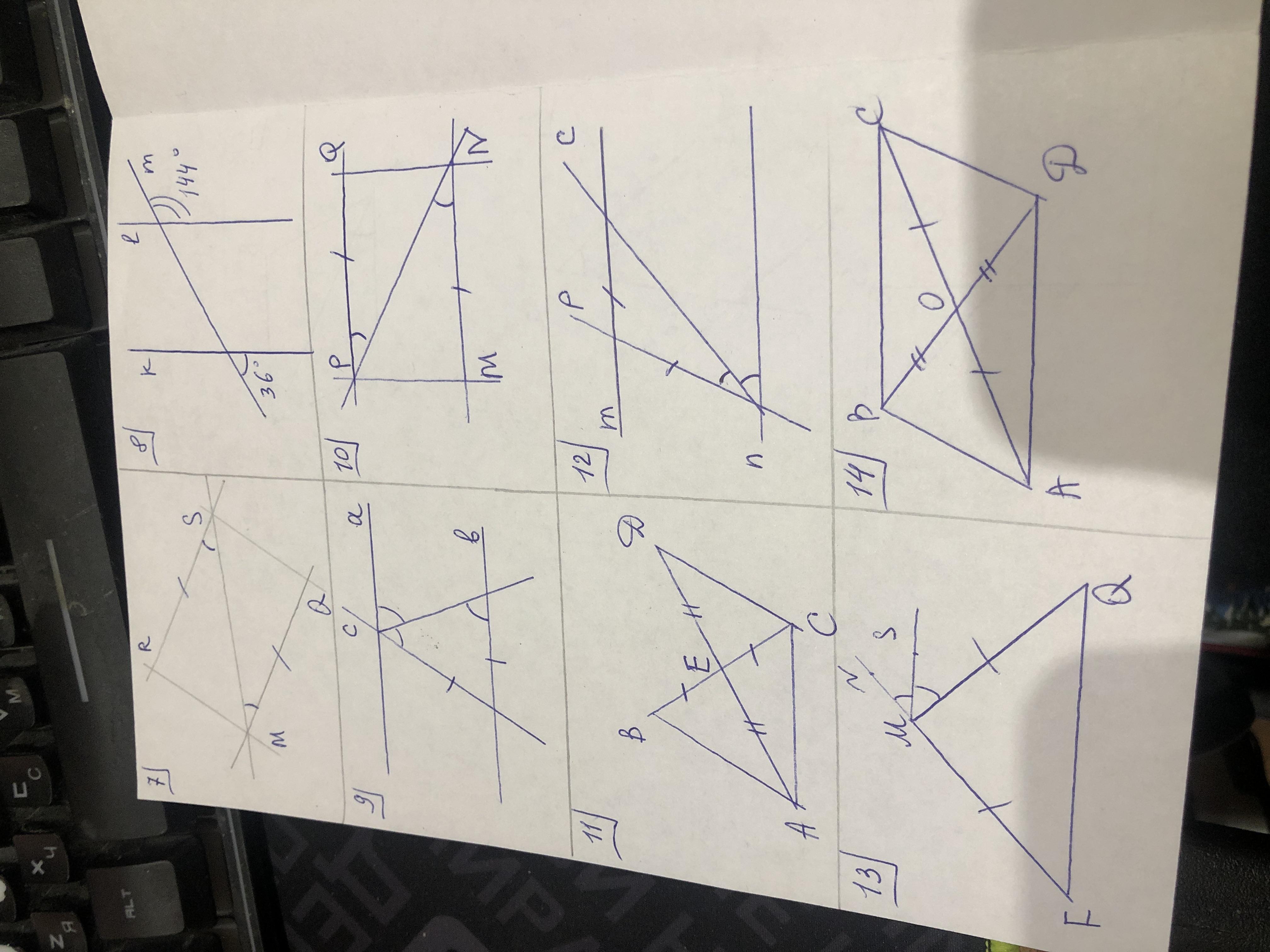
7) RS || MQ, RM || SQ
отрезок MS — общий для ΔSRM и ΔMQS. Данные треугольники равны по первому признаку равенства треугольников:
∠RSM = ∠QMS — как накрест лежащие при RS || MQ
∠RMS = ∠QSM — как накрест лежащие при RM || SQ
8) m || n
равны соответствующие углы (по 36° и 144°), и сумма односторонних равна 180° (144+36).
9) a || b
равны накрест лежащие углы (по свойству биссектрисы угла и равнобедренного треугольника)
10) PQ || MN, PM || QN
отрезок PN — общий для ΔPQN и ΔNMP. Данные треугольники равны по первому признаку равенства треугольников:
∠QPN = ∠MNP — как накрест лежащие при PQ || MN
∠QNP = ∠MPN — как накрест лежащие при PM || QN
11) BA || DC
∠BEA = ∠CED как вертикальные ⇒ ΔBEA равен ΔCED по первому признаку равенства треугольников (две стороны и угол между ними)
Пары углов (∠EDC = ∠EAB) и (∠EBA = ∠ECD) — как накрест лежащие
12) m || n
равны накрест лежащие углы (по свойству биссектрисы угла и равнобедренного треугольника)
13) MS || FQ
MS — биссектриса ∠NMQ. Угол ∠NMQ — внешний для вершины M равнобедренного треугольника MFQ. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним ⇒ ∠MFQ = ∠MQF = ∠NMS = ∠SMQ.
∠SMQ = ∠MQF — как накрест лежащие
14) BC || AD, BA || CD
Пары углов (∠BOA = ∠DOC) и (∠BOC = ∠DOA) как вертикальные ⇒ ΔBOA равен ΔDOC и ΔBOC = ΔDOA по первому признаку равенства треугольников.
∠OBC = ∠ODA и ∠OCB = ∠OAD — как накрест лежащие при BC || AD
∠OBA = ∠ODC и ∠OAB = ∠OCD — как накрест лежащие при BA || CD
Ответ: во вложении Объяснение:


