Предмет: Алгебра,
автор: marina030304
Тригонометрия, 9 класс.
Со всеми решениями, пожалуйста.
Вариант Б2. Буквы б в номерах 1 и 2
Приложения:
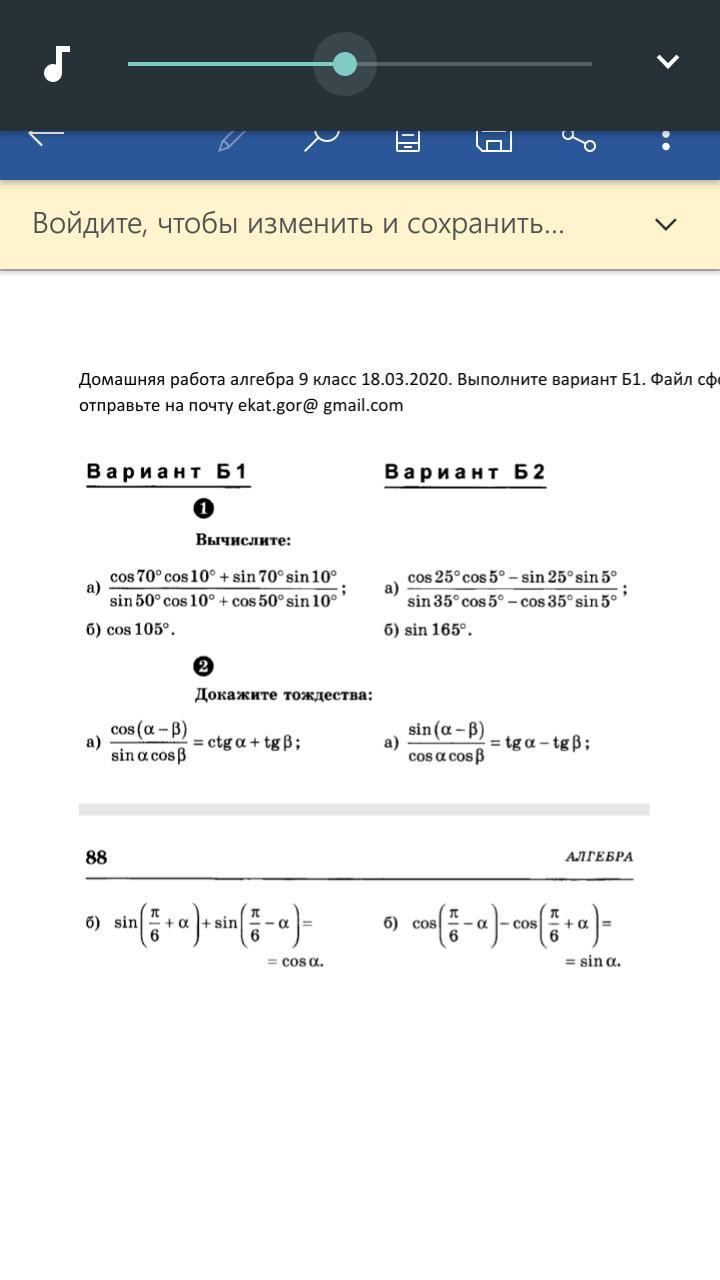
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Seagull24
Предмет: Қазақ тiлi,
автор: Musik14
Предмет: Английский язык,
автор: Sveta334
Предмет: Алгебра,
автор: 1234554321c