Предмет: Алгебра,
автор: ВладимирБ
Решить уравнение
.....................................
Приложения:
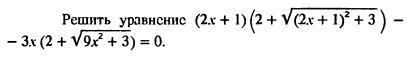
Ответы
Автор ответа:
4
Перенесем выражение со знаком минус в правую часть.
Имеем: ; Пусть
.
. Более того, наша функция непрерывна и определена на всем множестве действительных чисел. Итак,
монотонна. Уравнение можно переписать:
; В силу монотонности:
;
Ответ: x=1
Simba2017:
лихо вы расправились)
Похожие вопросы
Предмет: Английский язык,
автор: habzei
Предмет: Русский язык,
автор: никита2160
Предмет: Українська мова,
автор: lana1829
Предмет: Литература,
автор: ютубер845
Предмет: Литература,
автор: даша2851