Предмет: Алгебра,
автор: Аноним
Это просто какой-то капец... Решите и это, пожалуйста:
4tgx - 3ctgx + 11 = 0.
Дедлайн до завтрашнего утра......
necodancer:
дели на ctg
и решай квадратное уравнение
Ответы
Автор ответа:
1
Вот решение с помощью замены
Приложения:
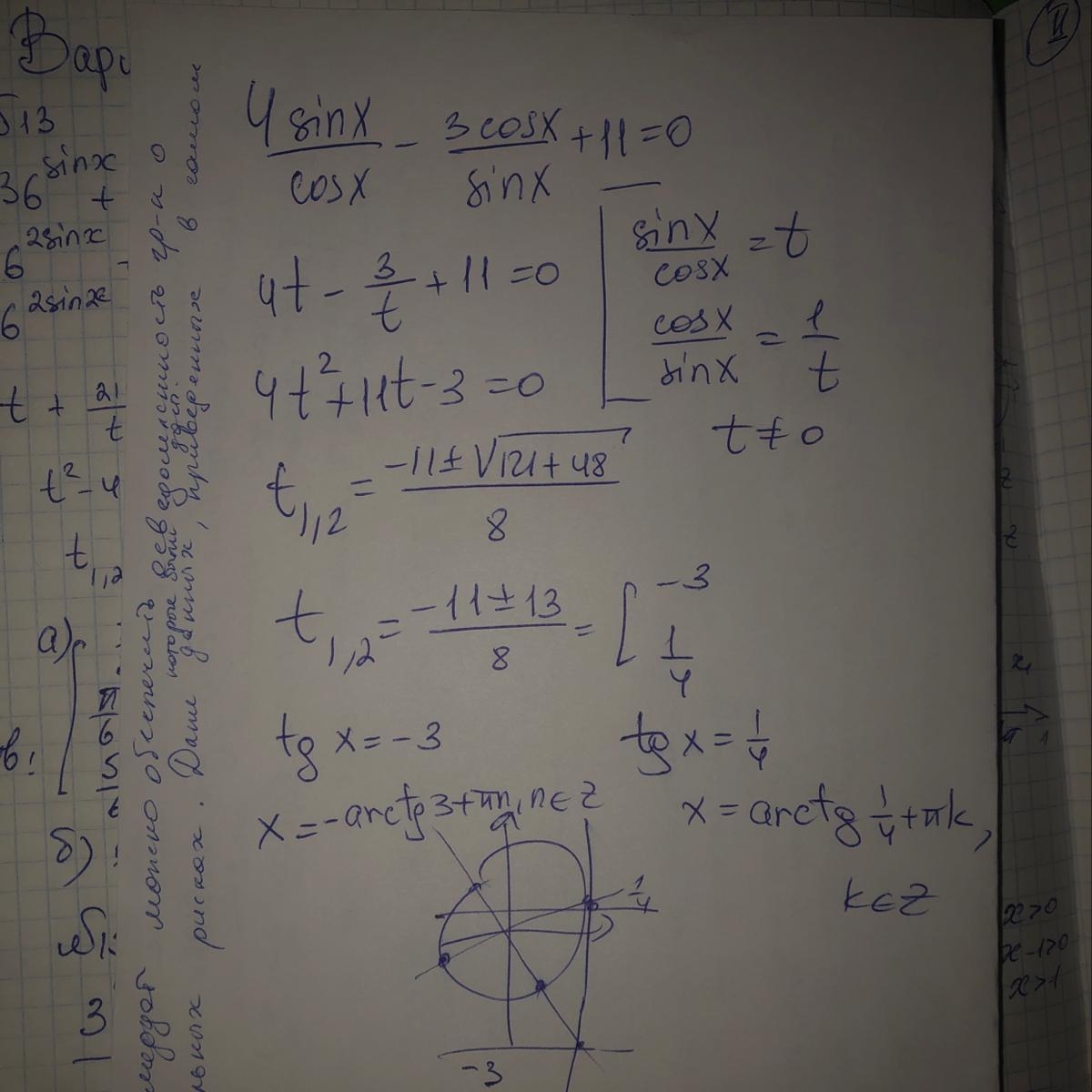
ОДЗ не влияет на полученные корни. У меня там тоже есть ОДЗ t≠0, но таких корней не оказалось, так что всё в порядке.
Да, потому что sinx, cosx не равны нулю
На ответ это никак не влияет, но если будешь чертить окружность, то точки просто выкалываются
На ответ это никак не влияет, но если будешь чертить окружность, то точки просто выкалываются
В университете будет сложнее, я как студент Вам говорю.
В университете понадобится. В архитектуре понадобится. В медецине и биологии понадобится. Она применяется во многих разделах математики и физики.
Медицина*
Автор ответа:
1
Так как , то
Сделаем соответствующую замену:
Обратная замена:
Ответ:
; )
Похожие вопросы
Предмет: Українська мова,
автор: Лилия421
Предмет: Русский язык,
автор: Zlatovlolosaya
Предмет: Русский язык,
автор: stepanovajulij
Предмет: Физика,
автор: Феич