Допоможіть ще)) Будь-ласка
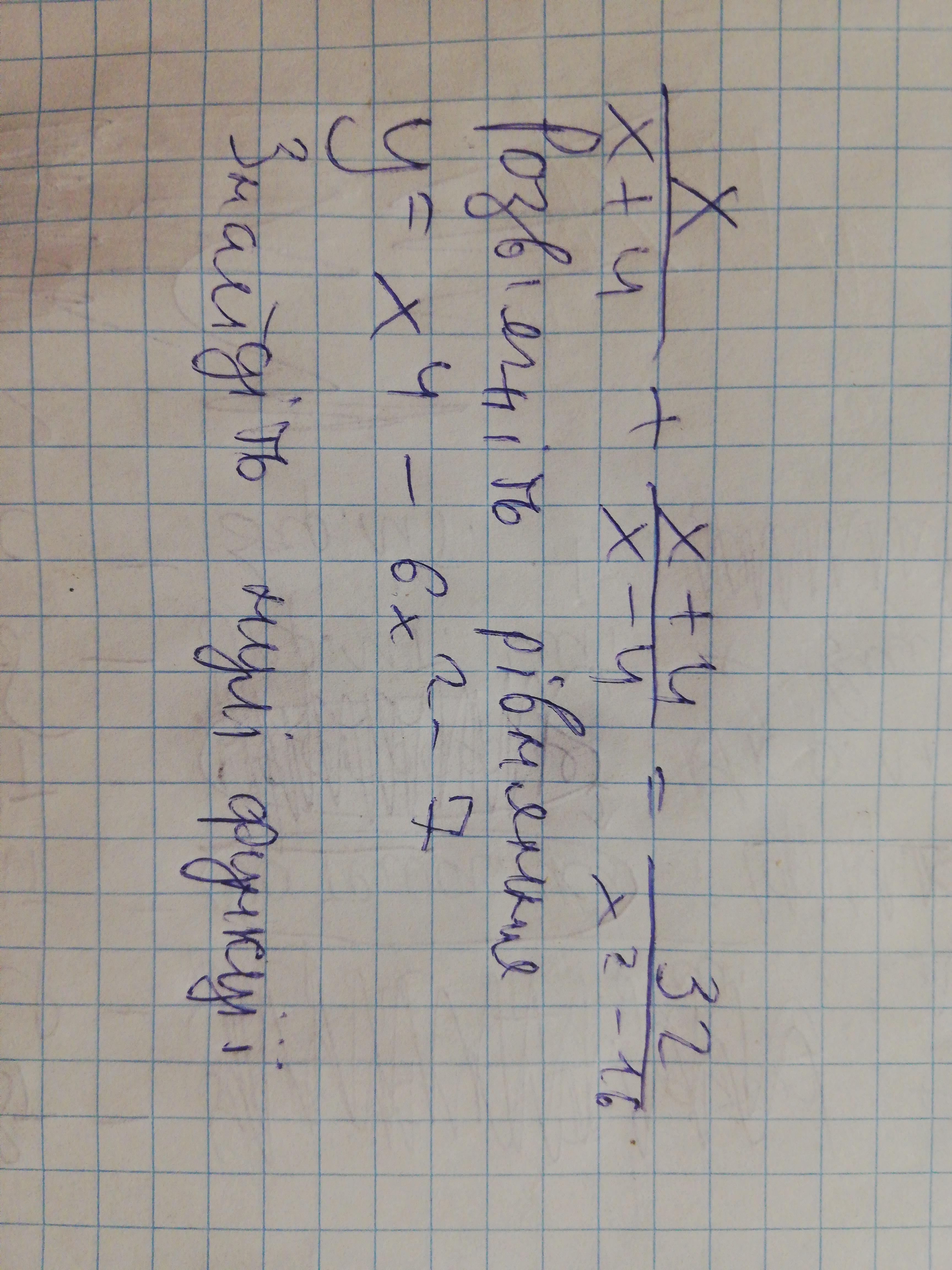
Ответы
Ответ:
Объяснение:
ОДЗ: x+4≠0 x≠-4 x-4≠0 x≠4.
x=4 ∉ОДЗ. ⇒
Ответ: уравнение решения не имеет.
x не имеет действительных корней.
Ответ: (-√7;0) (√7;0).
https://znanija.com/task/34691052
1) Решить уравнение x /(x+4) +(x+4) / (x-4) = 32 /(x² -16) .
2) Найти нули функции у = x⁴ - 6x² - 7 .
Ответ: 1) 2 ; 2) { -√7 ; √7 } .
Объяснение:
1) x /(x+4) +(x+4) / (x-4) - 32 / x /(x+4) +(x+4) / (x-4) = 32 /(x² -16) = 0 ;
( x(x - 4) +(x+4)² -32 ) / (x- 4)(x+4) ;
( x² - 4x+ x²+8x +16 -32 ) / (x- 4)(x+4) ;
2( x² +2x -8 ) / (x- 4)(x+4) =0 ОДЗ : x ≠ ± 4
x² +2x -8 =0 ⇒ x₁ = - 4 →посторонний корень ; x₂ = 2
----------------
2) у = x⁴ - 6x² - 7
(x²)² - 6x² - 7 =0 квадратное уравнение относительно x²
x² =3 ± 4
Или проводим замену : t = x² ≥ 0
t² - 6t - 7 =0 ⇒ t₁ = - 1 , t₂ = 7 по т Виета
(t₁ = - 1 < 0→посторонний корень)
обратная замена x² =7 ⇒ x =±√7
ИЛИ
t² - 6t - 7 =0
D₁ = D/4 =(-6/2)² -(-7) =9+7 =16 = 4² , √D₁ =4
t ₁,₂ =3 ±√D₁ =3 ± 4
t₁ = - 1 →посторонний корень ,
t₂ = 7
* * * * * * * * * * *
(x²)² - 6x² -7 =0 ⇔(x²)² - 7x² + x² -7 =0 ⇔x²(x²-7) +(x²-7) =0 ⇔
(x²-7)(x²+1) =0⇔ (x²-7)(x²+1) =0 || x²+1 ≥ 1≠0 ||
x² - 7 = 0 ⇔ (x -√7)(x+√7) = 0 ⇒x₁ =√7 ; x₂ =- √7 .