Question

В треугольнике MNK MN = NK. Точки А, В и С - середины сторон МК, MN и NК соответственно. Докажите что угол (знак) MBA = углу (знак) KCA.

Answer 1

Не совсем понятно, для чего дан именно равнобедренный треугольник .   При данном расположении точек, делящих стороны на две равные части, в любом треугольнике, не только равнобедренном, верно равенство ∠ MBA = ∠ KCA 
Решение:
В на MN,
C на NK 
А на МК -делят стороны треугольника на равные части ( пополам) и потому 
АВ и АС - средние линии этого треугольника.
 Отсюда следует их параллельность соответственным сторонам. 
Из равенства углов, образованных  при параллельных прямых секущей,
следует, что
∠ МВА=∠МNK 
∠ACK=∠MNК
.Если два угла по отдельности равны третьему - они равны между собой. 
∠ MBA = ∠ KCA, что и требовалось доказать.
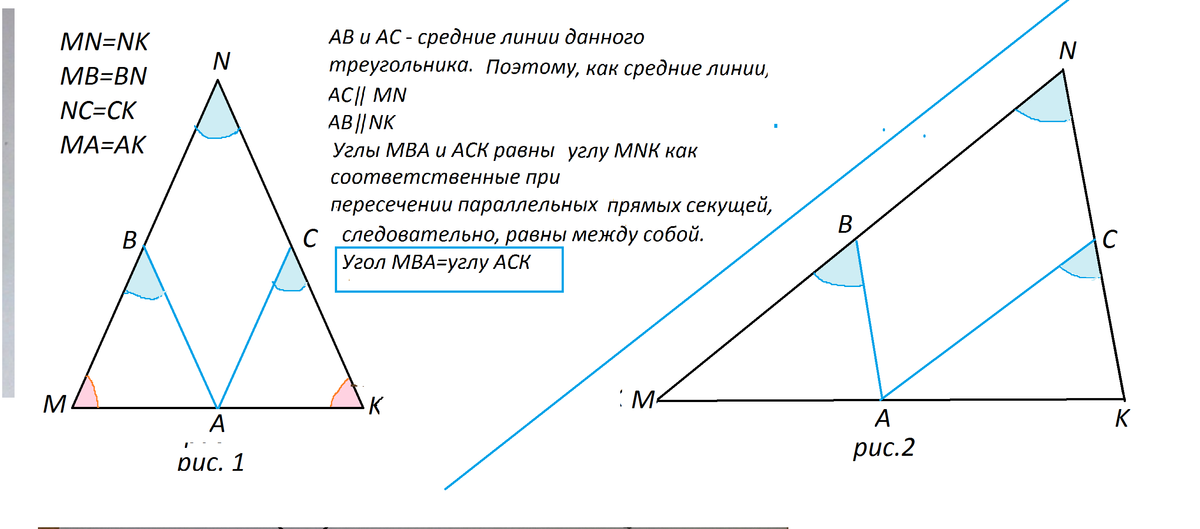
 См. рисунки. Рисунок 1 - по условию. 
Рисунок 2 - как иллюстрация решения для любого треугольника.