Предмет: Алгебра,
автор: OrangeOI
(ln^2x)/x dx
(дробь логарифм в квадрате от икс деленный на икс все это по dx)
определенный интеграл, пределы интегрирования от 0 по е
Ответы
Автор ответа:
0
Несобственный интеграл расходится
OrangeOI:
спасибо, мне это не надо было правда
а зачем вопрос тогда задавали ? Если бы написан был нижний предел 1, то не было бы несобственного интеграла, а был обыкновенный определённый интеграл...Зря писала ?
ну да я вместо 1 0 написал пришлось другой вопрос задавать
а спасибо за мои труды не надо? ещё будешь несобственные интегралы проходить, пригодится...
Автор ответа:
0
Ответ: я так понял, пределы от 1 до е, Объяснение:
Приложения:
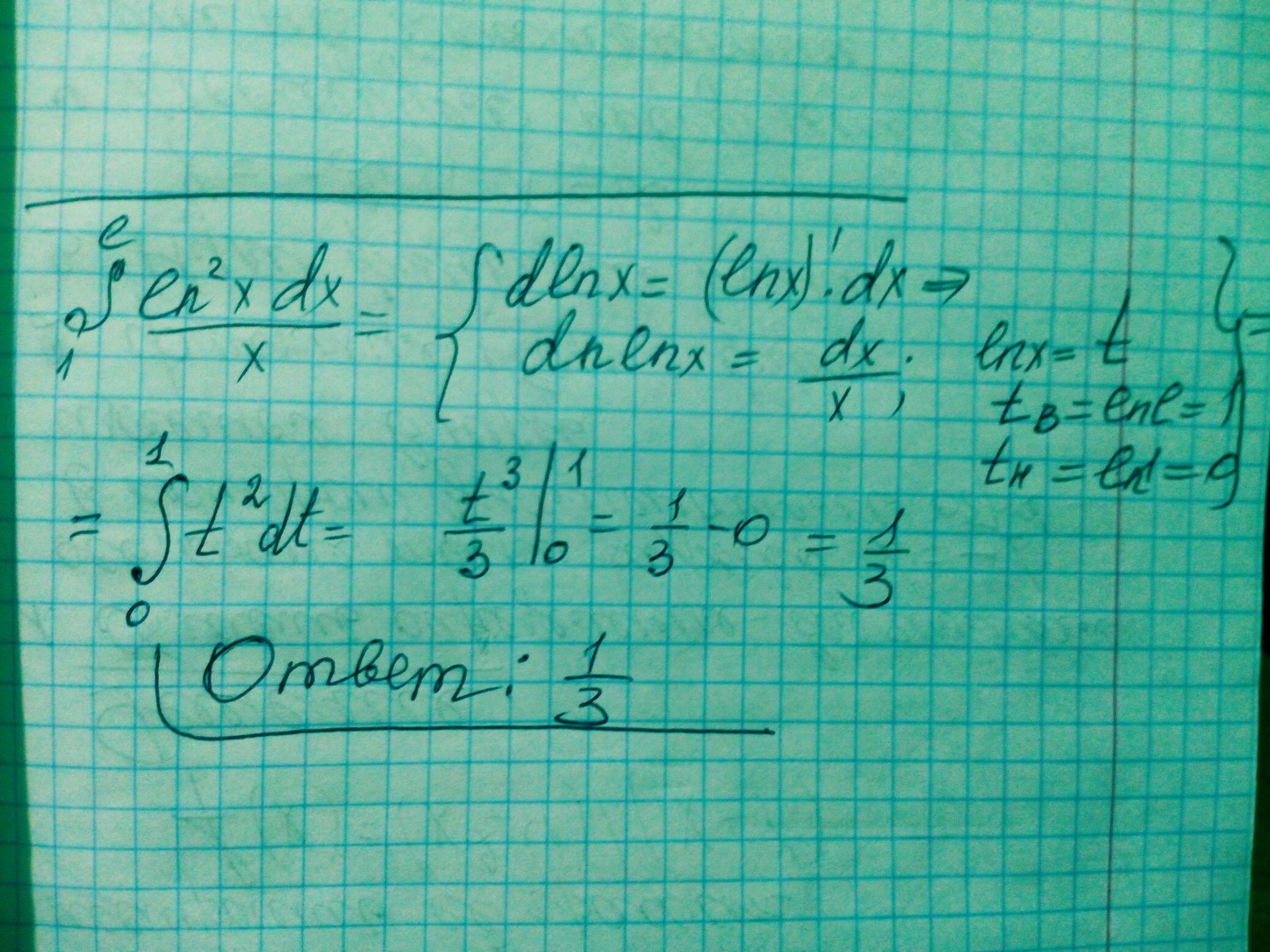
Похожие вопросы
Предмет: Другие предметы,
автор: НаСтАсЬкА007
Предмет: Українська мова,
автор: nikitatan
Предмет: Русский язык,
автор: mimifaca
Предмет: Геометрия,
автор: Fefedor
Предмет: Химия,
автор: vika7474