Предмет: Математика,
автор: iuriimode
ФУНКЦИИ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ: Найти полный дифференциал функции двух
переменных. Пожалуйста помогите решить.
Приложения:
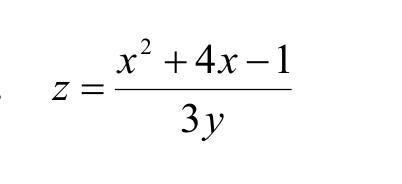
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
iuriimode:
Спасибо большое !)
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: tatulja
Предмет: Другие предметы,
автор: kira0513
Предмет: Геометрия,
автор: vika12345101