Предмет: Алгебра,
автор: Lehamishin4
помогите плз алгебра 10-11 класс
Приложения:
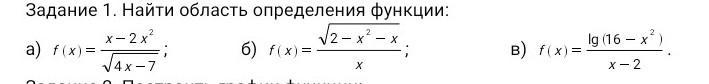
Ответы
Автор ответа:
1
NNNLLL54:
перезагрузи страницу...
уже несколько раз
ну, это технические неполадки от меня не зависящие...перезагружаться надо не с телефона...
так
я открыл с браузера всё норм
но можно чуть поподробнее
добавила
спасибо большое
спасли меня
спасибо на кнопочке нажми
Автор ответа:
0
Ответ: приложено
Объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: alina140400
Предмет: Английский язык,
автор: нашкэ0990
Предмет: Русский язык,
автор: Kah
Предмет: Математика,
автор: Arturchik228
Предмет: Алгебра,
автор: shnayder86