Предмет: Алгебра,
автор: karakatiz
Решить дифференциальное уравнение:
Приложения:
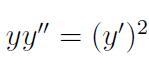
Ответы
Автор ответа:
0
Тип: дифференциальное уравнение второго порядка, допускающее понижения порядка.
Пусть , тогда
, получаем
Выполним обратную замену
Если u = 0, то
Ответ: или
karakatiz:
Могу вас попросить глянуть другие уравнения, заданные мною?
Если не срочно, то могу через мин 20 глянуть
Хорошо. Буду благодарен.
Похожие вопросы
Предмет: Українська мова,
автор: кивон
Предмет: Русский язык,
автор: Olarena
Предмет: Русский язык,
автор: lenka89999
Предмет: География,
автор: Щалащвщсла
Предмет: Математика,
автор: klyuchkinataty