Предмет: Алгебра,
автор: karakatiz
Решить дифференциальное уравнение:
Приложения:
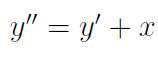
Ответы
Автор ответа:
0
Тип: дифференциальное уравнение второго порядка, допускающее понижения порядка.
Пусть , тогда
, получаем :
Умножим обе части уравнения на , получаем
Интегрируем обе части уравнения
В правой части уравнения интеграл будем считать путём интегрирования по частям
Выполним обратную замену
Ответ: .
Похожие вопросы
Предмет: Русский язык,
автор: 325252reht
Предмет: Українська мова,
автор: creAtivka
Предмет: Другие предметы,
автор: kakulykakuly123
Предмет: Геометрия,
автор: anonim5551