Предмет: Математика,
автор: bijers
1) Найти наименьшее и наибольшее значения функции  на отрезке [−7;9].
на отрезке [−7;9].
2) Найти наибольшее и наименьшее значения функции 
sharofat0:
для первого задания указан отрезок, значит нужно найти зничение функции на его концах и сравнить?
конечно, во втором тоже, у вас найдены локальные максимумы и минимумы, но никак не наибольшее и наименьшее значения
Я не савсем поняла один отрезок на оба пункта? Спасибо за помощь!
нет, там отрезок только для первого пункта
Тогда получается ,что функция не ограничена снизу и не ограничена сверху?Такие вещи я могу делать по графику, а без графика?
Пожалуйста, помогите разобраться!
посмотрите мое решение, ниже
Спасибо, для меня это очень важно!
Ответы
Автор ответа:
3
Ответ:
Найти наибольшее и наименьшее зн.
функции на отрезке.
Приложения:

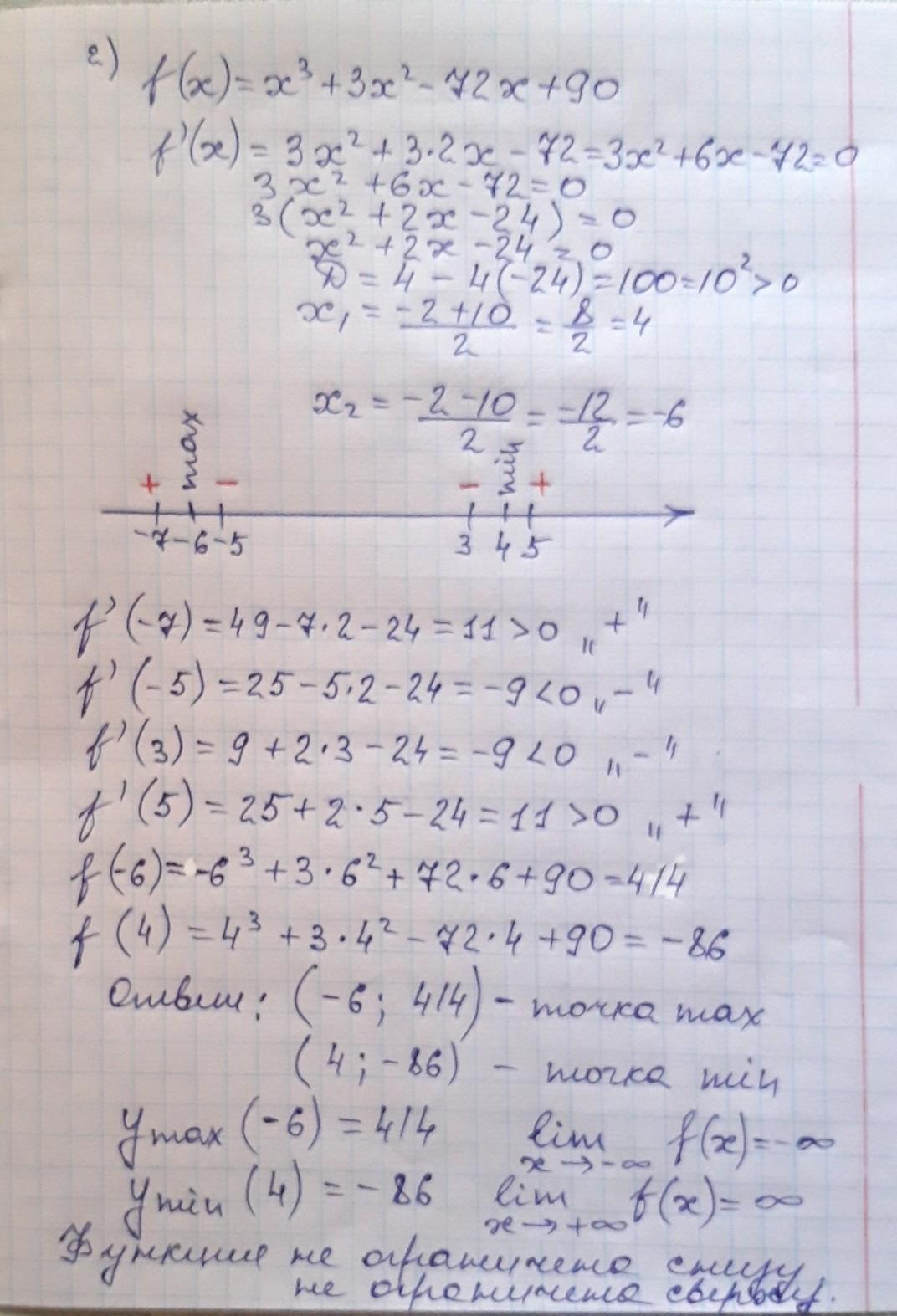
вы нашли точки максимума и минимума, а не наибольшее и наименьшее значение
Автор ответа:
2
Ответ:
Пошаговое объяснение:
1) y' = 3x² + 6x - 9
y' = 0
x² + 2x - 3 = (x + 3)(x - 1) = 0
x₁ = -3; x₂ = 1
y(-7) = -135 - наименьшее значение
у(-3) = 25
у(1) = -7
у(9) = 889 - наибольшее значение
2)
f'(x) = 3x² + 6x - 72
f'(x) = 0
x² + 2x - 24 = (x+ 6)(x - 4) = 0
x₁ = -6; x₂ = 4
f(-6) = 414
f(4) = -86
нет наибольшего и наименьшего значения
найденные точки - точки локального минимума (x = 4) и максимума(x = -6)
Похожие вопросы
Предмет: Русский язык,
автор: Лена21
Предмет: Русский язык,
автор: Anna100000
Предмет: Русский язык,
автор: lais
Предмет: Математика,
автор: кликая1234567890