Предмет: Алгебра,
автор: Аноним
Задачи на математическую индукцию. Найти сумму в обоих пунктах (через формулу). Написать нормальное решение( База, переход)
Даю 50 баллов.
Приложения:
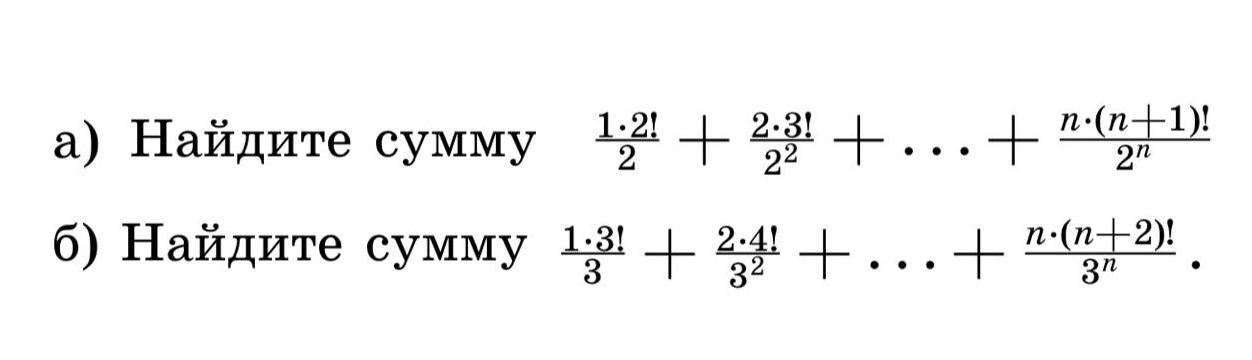
Аноним:
не знаете- не пишите. Буду банить за флуд.
ну я же правильно сделал а второе не знаю как решить
нет
это неправильно.
А причем тут математическая индукция?
А понял)
Ответы
Автор ответа:
1
a) Покажем, что
Докажем равенство методом математической индукции
База индукции справедливо:
. Допустим, что равенство
справделиво, и докажем, что оно влечет равенство
Действительно,
Следовательно, равенство имеет место для любого
б) Аналогично, доказывается
Второй пункт для самостоятельного упражнения.
спасибо большое!
Похожие вопросы
Предмет: Русский язык,
автор: Varya0
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: 0962706567
Предмет: История,
автор: maniss
Предмет: Математика,
автор: mariyamotko