Question

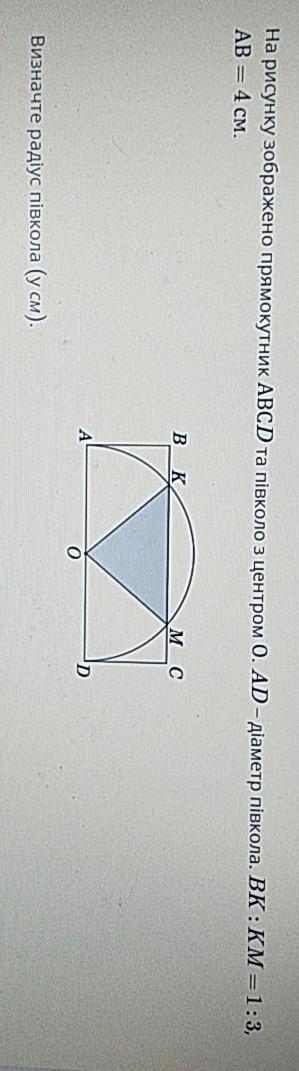
На рисунку зображено прямокутник АВСD та півколо з центром О. АD-діаметр півкола. ВК : КМ= 1:3, АB - 4 см. знайти радіус півкола​

Answer 1

Проведём высоту OH к стороне основания KM треугольника KOM. Треугольник KOM является равнобедренным, поскольку KO = MO (как радиусы полуокружности). Значит, OH - медиана и биссектриса.

Пусть BK = x см, а KM = 3x см, тогда BM = 4x см.

KH = 3x/2, тогда KO = MO = AO = BH = x + 3x/2 = 5x/2 см

По теореме Пифагора из прямоугольного треугольника KOH:

$KO^2=KH^2+OH^2\\ \\ \left(\dfrac{5x}{2}\right)^2=\left(\dfrac{3x}{2}\right)^2+4^2\\ \\ \left(\dfrac{5x}{2}-\dfrac{3x}{2}\right)\left(\dfrac{5x}{2}+\dfrac{3x}{2}\right)=16\\ \\ x\cdot 4x=16\\ \\ x^2=4\\ \\ x=2$

Следовательно, радиус полуокружности: $KO=\dfrac{5\cdot2}{2}=5$ см