Предмет: Алгебра,
автор: ravilkornikov0328
Найти силовое значение выражения
Приложения:
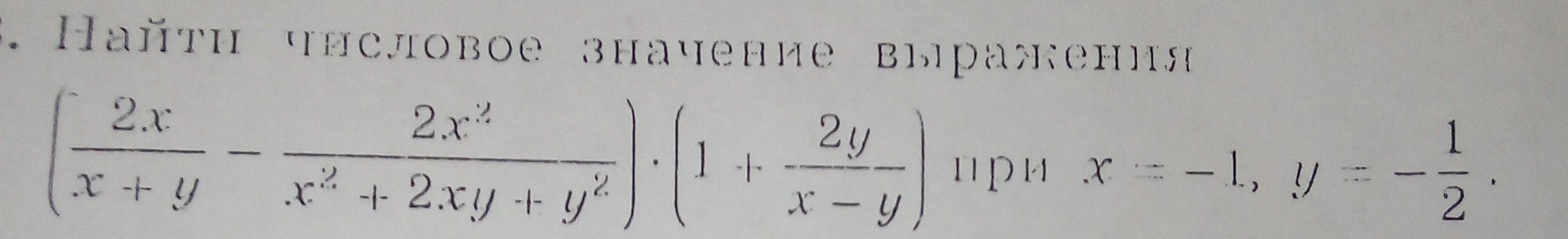
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: tatyanamelnikov
Предмет: Русский язык,
автор: 3336
Предмет: Другие предметы,
автор: edin36
Предмет: Биология,
автор: alionakovtun444