Найти площадь правильного треугольника описанного вокруг окружности, если площадь правильного шестиугольника описанного вокруг окружности равна 36 см кв
Ответы
Ответ: 54 см²
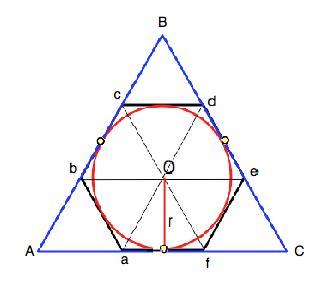
Объяснение: Сделаем чертеж и обозначим вершины шестиугольника a, b, c, d, e и f.
Правильный шестиугольник диагоналями, проведенными через его центр О, делится на шесть равных правильных треугольников. Если продолжить его стороны bc, de и af до пересечения в точках А, В и С, получится правильный треугольник АВС, описанный около данного шестиугольника и около той же окружности. Треугольники, получившиеся на трех противоположных сторонах шестиугольника - правильные (внутренние углы в правильном шестиугольнике равны 120°, смежные с ними равны 60°). Длина стороны ∆ АВС в 3 раза больше стороны шестиугольника. Имеем 6 правильных треугольников в шестиугольнике и 3 правильных - вне его, всего 9..
S (ABC)=S(abcdrf)•9/6=9•36:6=54 см²,
т.е.