Question

Найти наименьший из острых углов прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 2 : 1.

Answer 1

Ответ:

30°

Объяснение:

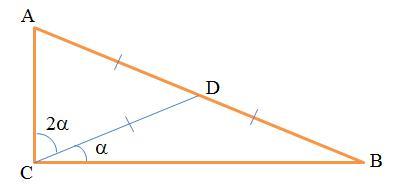
Дано (см. рисунок):

 ΔABC

 ∠C=90°

 CD - медиана

 ∠ACD:∠DCB=2:1  

Найти: наименьший из острых углов прямоугольного треугольника.

Решение.

Обозначим ∠DCB через α. Тогда ∠ACD=2α и

∠C=90°=∠ACD+∠DCB=2α+α=3α. Отсюда α=90°:3=30°.

Как известно, медиана, проведённая к его гипотенузе равна половине гипотенузы, то есть CD=AB:2, следовательно треугольник CDB равнобедренный. По свойству равнобедренных треугольников углы при основании равны, в нашем случае ∠B=∠DCB=30°.

Тогда ∠A=90°-∠B=90°-30°=60°.

Значит ∠A > ∠B.