Question

ДАЮ 30 БАЛЛОВ!!!

1. Найдите угол треугольника, если два других угла равны 310 и 240.
2. Найдите углы треугольника, если их градусные меры относятся как 2 : 7 : 9.
3. Угол при основании равнобедренного треугольника равен 290. Найдите остальные углы этого треугольника.
4. Найдите углы равнобедренного треугольника, если угол при основании в 7 раз меньше угла при вершине.
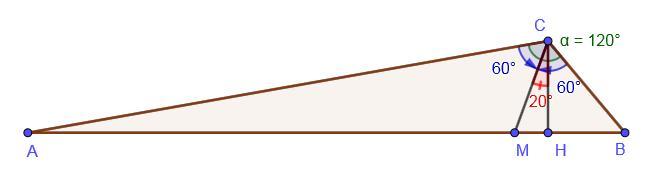
5. Один из углов треугольника равен 1200. Высота и биссектриса, проведенные из вершины этого угла, образуют угол, равный 200. Найдите неизвестные углы треугольника.

Answer 1

1. Сумма углов треугольника — 180°

∠x = 180−(31+24) = 180−(55) = 125°

Ответ: 125°.

2. Выразим углы через х, сумма углов = 180°. составим и решим уравнение:

    2x+7x+9x = 180

    18х = 180

    х = 10

∠1 = 2х = 2·10 = 20°

∠2 = 7х = 7·10 = 70°

∠3 = 9х = 9·10 = 90°

Ответ: 20°, 70° и 90°.

3. Угли при основании равнобедренного треугольника равны (∠1 = ∠2 = 29° ). Найдем угол вершины:

∠3 = 180−(∠1 +∠2 ) = 180−(2·29) = 180−58 = 122°

Ответ: 29°, 122°.

4. Обозначим углы через х. Пусть углы при основании равны х° (равны по свойству равнобедренного Δ), тогда угол при вершине — 7х. Сумма углов равна 180°. Составим и решим уравнение:

   2x+7x = 180

   9x = 180

   x = 20

Углы при основании х — по 20°.

Угол при вершине: 7х = 7·20 = 140°.

Ответ: углы при основании — по 20°, угол при вершине —  140°.

5. Дан ΔABC, АВ — основание, ∠C = 120°, CM — биссектриса из вершины C, СН — высота из вершины С, ∠MCH = 20°. Найти ∠A и ∠B.

∠ACM = ∠ MCB = 120/2 = 60° — по свойству биссектрисы.

∠HCB = ∠MCB−MCH = 60−20 = 40°.

∠CHB = 90° ⇒ ∠B = 180−(∠CHB+∠HCB) = 180−(90+40) = 180−130 = 50°.

∠A = 180−(∠C+∠B) = 180−(120+50) = 180−170 = 10°.

Ответ: 50° и 10°.