Предмет: Алгебра,
автор: abdullamuftahutdinov
Решите пожалуйста! Даю 10 баллов
Приложения:
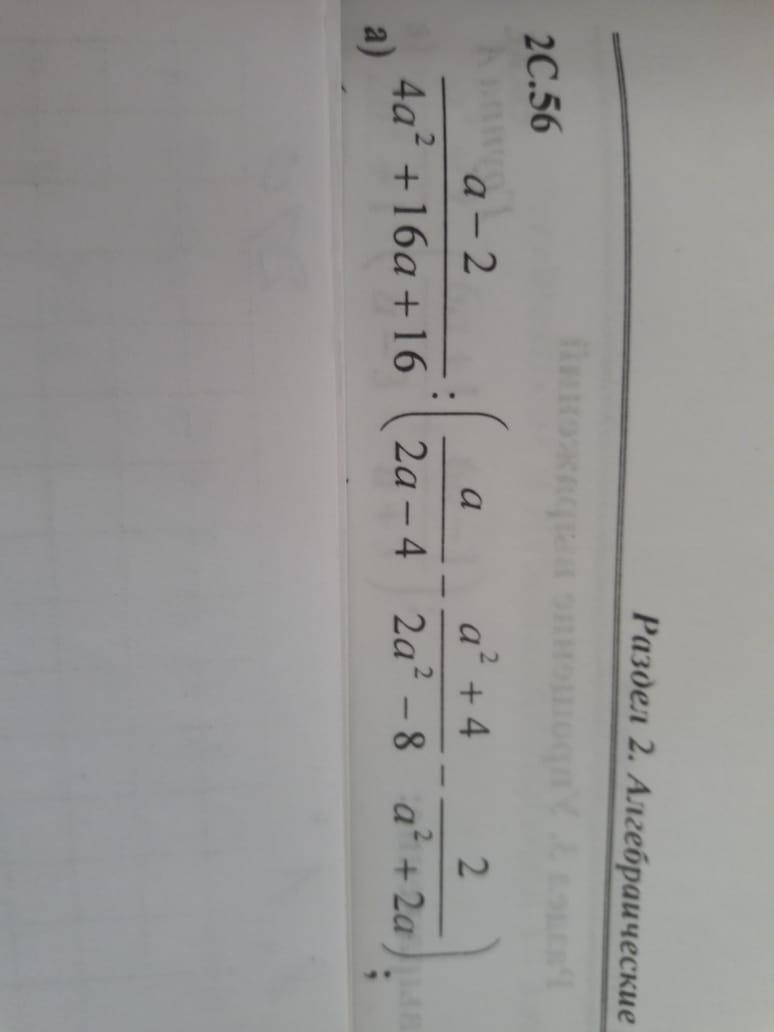
Ответы
Автор ответа:
0
Решение во вложении:
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: Жанна1705
Предмет: Английский язык,
автор: стерх
Предмет: Русский язык,
автор: jetfly99
Предмет: Геометрия,
автор: Afaxriya2001
Предмет: История,
автор: zhenackatjev20