Предмет: Математика,
автор: nardzhiskhadzhieva
Помогите!!! 30 баллов!
Приложения:
Ответы
Автор ответа:
1
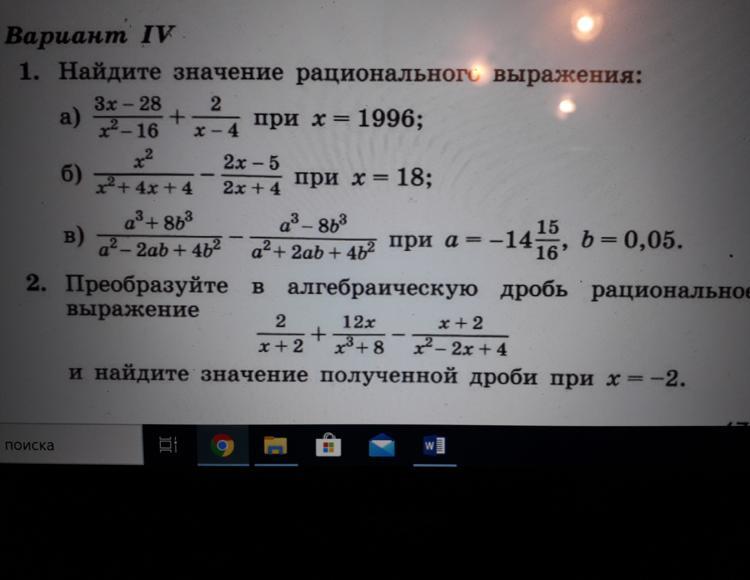
1. a)
b)
c)
2. Выражение при х=−2 не определено, т.к −2 не входит в область допустимых значений:
Все же, преобразуем выражение
Похожие вопросы
Предмет: Русский язык,
автор: trtrtrtrtrt1965
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Ангелинка2121
Предмет: Алгебра,
автор: ghgggc