Question

На приобретение обрудования для нового производственнного участка

выделено 200 тыс. руб.. Оборудование должно быть размещено на площади,

не превышающей 72 кв.м.. Предприятие может заказать оборудование двух

видов: машины типа А стоимостью 50 тыс.руб., требующие 6 кв.м площади (с

учетом проходов) и дающие 8 тыс.ед. продукции за смену, и машины типа В

стоимостью 20 тыс. руб., занимающие площадь 12 кв.м и дающие за смену 3

тыс.ед. Найти оптимальный вариант приобретения обрудования,

обеспечивающий максимум общей производительности нового участка.

а) Записать математическую модель задачи.

б) Решить задачу графическим методом​

Answer 1

Математическая модель:

$\displaystyle\begin{cases}50x_1+20x_2\leq200\\6x_1+12x_2\leq72\\x_i\geq0;x_i\in Z;i=1,2\end{cases}\\F=8x_1+3x_2\to max$

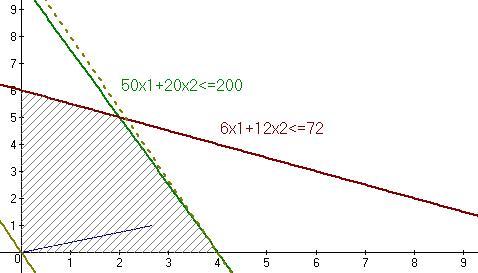
Графический метод: строим на графике функции ограничений, получаем область допустимых решений (ОДР). Далее строим линии уровня целевой функции(на рисунке - желтая линия), которую двигаем в направлении градиент - вектора(фиолетовая линия) (т.к. ищем максимум), до тех пор, пока не достигнем крайней точки ОДР. Крайняя точка ОДР и будет являться оптимумом. В данном случае это точка (4;0). И значение F равно 32 тыс. ед. продукции