Question

Разбиритесь в задаче, обьясните пожалуйста и запишите свои мысли и рассуждения на счет жтой задачи, очень нужно заранее большое спасибо... Я должна это понять.

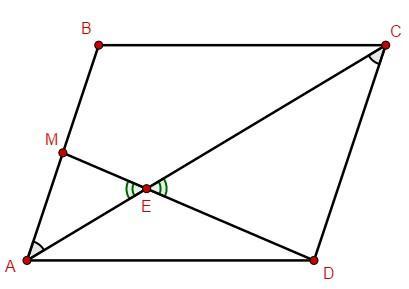
Диагональ АС параллелограмма АВСD равна 18 сантиметров. Середина М стороны АВ соединнена с вершиной D. Найдите отрезки, на которое делится диагональ АС отрезка DM. ​

Answer 1

Поскольку $M$ - середина стороны $AB$, значит $AM=MB$.

$\angle BAC=\angle ACD$ как накрест лежащие при $AB\parallel CD$ и секущей $AC$.

$\angle MEA=\angle CED$ как вертикальные;

Треугольники $AME$ и $CDE$ подобны по двум углам. Из подобия треугольников следует пропорциональность соответствующих сторон

$\dfrac{AM}{CD}=\dfrac{ME}{DE}~~\Rightarrow~~ \dfrac{ME}{DE}=\dfrac{1}{2}$

$\dfrac{ME}{DE}=\dfrac{AE}{CE}~~\Rightarrow~~\dfrac{1}{2}=\dfrac{18-CE}{CE}~~\Rightarrow~~ \dfrac{1}{2}=-1+\dfrac{18}{CE}~~\Rightarrow~~ CE=12$

Тогда AE = 18 - 12 = 6 см.

Ответ: 6 см и 12 см.