Предмет: Геометрия,
автор: arianamelkoian
Найдите длину стороны квадрата вписанного в круг радиус которого равен 5 см! Помогите, пожалуйста!
Ответы
Автор ответа:
3
Решение задания приложено
Приложения:
Автор ответа:
1
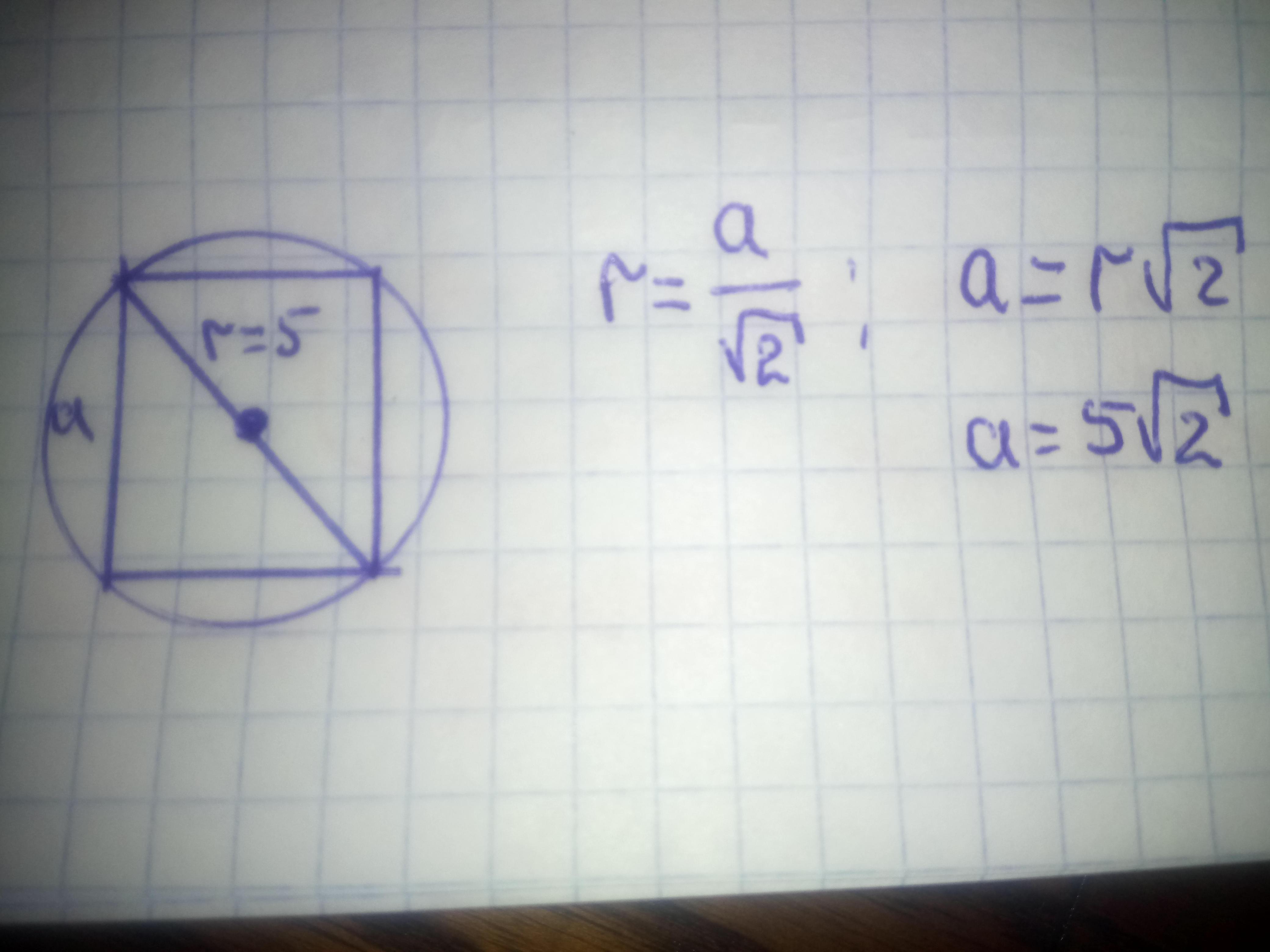
Если квадрат вписан в окружность, то все его главные 4 точки лежат на окружности, а значит диагональ квадрата будет является диаметром окружности, тогда длинна квадрата находится по формуле:
Поскольку радиусы равны, то х=у
Ответ:Длина стороны квадрата равна пяти квадратных корней из двух
Похожие вопросы
Предмет: Русский язык,
автор: dasha54321623657
Предмет: Английский язык,
автор: vazemiller00
Предмет: Русский язык,
автор: Ясинова
Предмет: История,
автор: помогайатосложно
Предмет: Экономика,
автор: Kuroo8Tetsurou