Question

Найти площадь треугольника со сторонами 25, 25 и 14. Определите радиусы вписанной и описанной окружности.

Answer 1

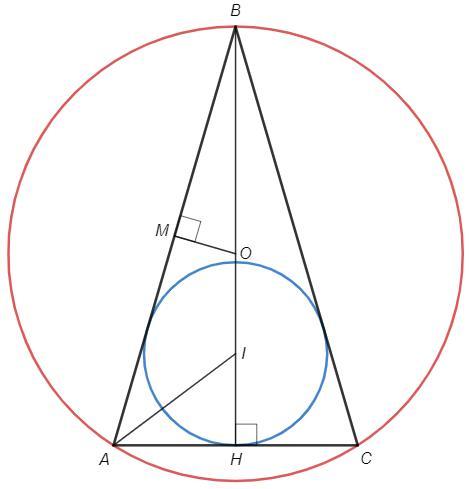
Равнобедренный треугольник, основание AC=14.

BH - высота к основанию, является также биссектрисой и медианой.

AH=AC/2 =7 (H - середина AC)

BH =√(AC^2 -AH^2) =24 (теорема Пифагора)

S(ABC) =AC*BH/2 =14*24/2 =168

Центр вписанной окружности (I) - точка пересечения биссектрис.

BI/IH =AB/AH =25/7 (теорема о биссектрисе)

IH =7/32 BH =21/4 =5,25

(IH - расстояние от центра до стороны, то есть радиус)

Центр описанной окружности (O) - точка пересечения серединных перпендикуляров.

M - середина AB, BM=25/2

△OBM~△ABH (по двум углам)

OB/AB =BM/BH

OB =25*25/2*24 =625/48  ~13,02