Question

Помогите пожалуйство очень срочно!!!
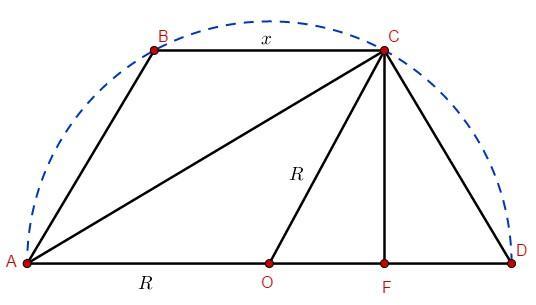
Вычислить наибольшую площадь трапеции, вписанной в полукруг радиуса R так, что нижним основанием трапеции служит диаметр полукруга

Answer 1

Если трапеция вписана в окружность то она равнобедренная. $\angle ACD=90^\circ$, поскольку он опирается на диаметр окружности. Следовательно, CO - медиана прямоугольного треугольника ADC и $CO=AO=OD=R$. Тогда $AD=2R$ и пусть $BC=x$.

$FD=\dfrac{AD-BC}{2}=\dfrac{2R-x}{2}=R-\dfrac{x}{2}$

$OF=OD-FD=R-\left(R-\dfrac{x}{2}\right)=\dfrac{x}{2}$

По теореме Пифагора из прямоугольного треугольника $COF$

$CF=\sqrt{R^2-\left(\dfrac{x}{2}\right)^2}=\dfrac{1}{2}\sqrt{4R^2-x^2}$

Рассмотрим функцию $S(x)=\dfrac{2R+x}{2}\cdot\dfrac{1}{2}\sqrt{4R^2-x^2}=\dfrac{(2R+x)\sqrt{4R^2-x^2}}{4},~~ 0\leq x\leq 2R$

$S'(x)=\dfrac{1}{4}\left(\sqrt{4R^2-x^2}+(2R+x)\cdot \dfrac{-2x}{2\sqrt{4R^2-x^2}}\right)=\\ \\ \\ =\dfrac{1}{4}\left(\sqrt{4R^2-x^2}-\dfrac{2Rx+x^2}{\sqrt{4R^2-x^2}}\right)=\dfrac{-2x^2-2Rx+4R^2}{4\sqrt{4R^2-x^2}}$

Приравниваем производную функции к нулю

$-\dfrac{2x^2+2Rx-4R^2}{4\sqrt{4R^2-x^2}}=0~~~\Rightarrow~~~ 2x^2+2Rx-4R^2=0\\ \\ \\ x^2+Rx-2R^2=0\\ \\ x^2+2Rx-Rx-2R^2=0\\ \\ x(x+2R)-R(x+2R)=0\\ \\ (x+2R)(x-R)=0$

$x_1=-2R$ — не принадлежит $x \in [0;2R]$

$x_2=R$

[0]____+____[R]____-_____[2R]

Функция на промежутке $x \in [0;R]$ возрастает, а затем на $x \in [R;2R]$ убывает, следовательно, $x=R$ - относительный максимум

$S(R)=\dfrac{(2R+R)\sqrt{4R^2-R^2}}{4}=\dfrac{3\sqrt{3}}{4}R^2$

Ответ: $\dfrac{3\sqrt{3}}{4}R^2$