Предмет: Алгебра,
автор: Jfvdvdhdj
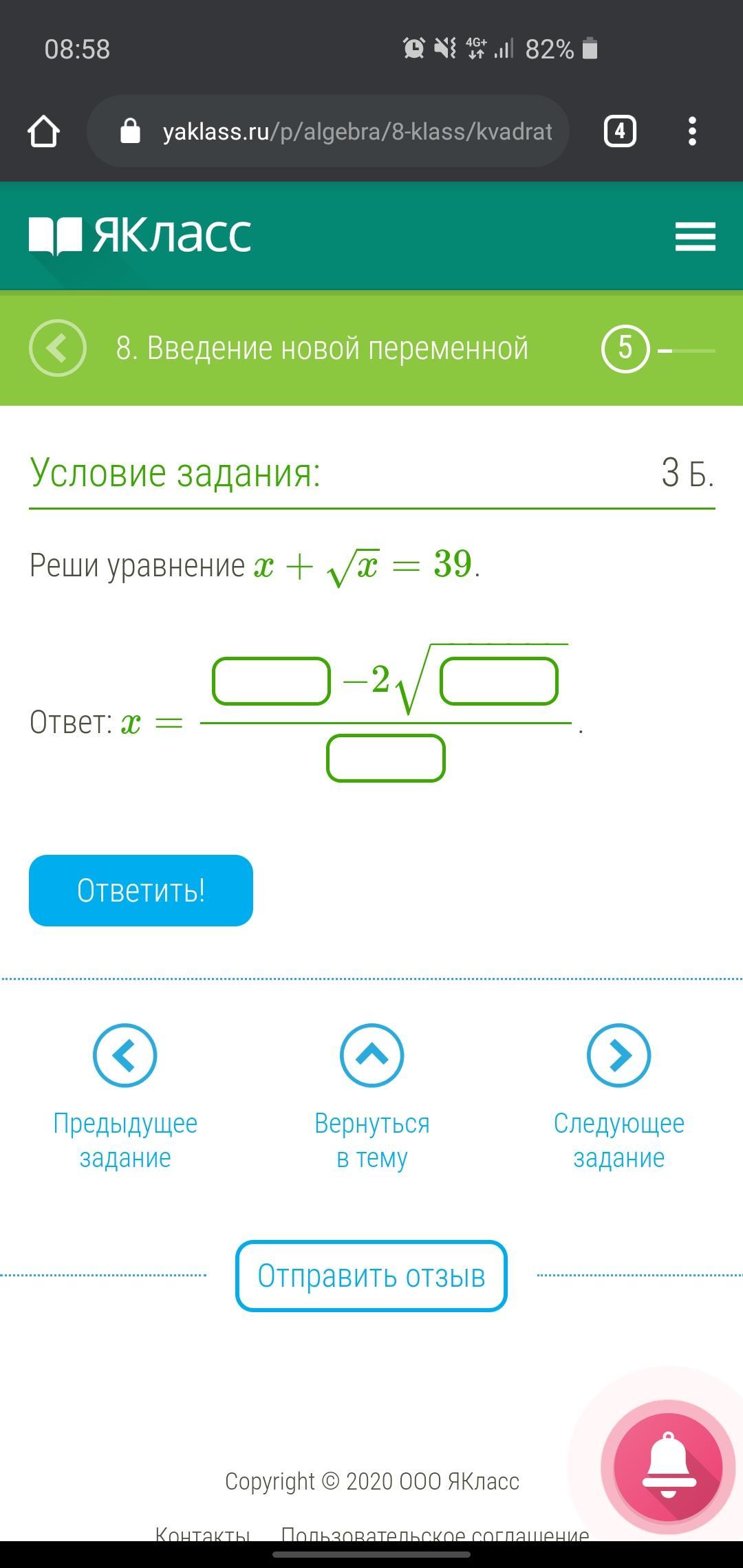
Не могли бы вы мне помочь с решением на приложенной картинке .
Приложения:
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: 1sroil
Предмет: Русский язык,
автор: асяяяяяяяяяяяяяяяяя
Предмет: Русский язык,
автор: Nan2001
Предмет: История,
автор: Nastenka5704
Предмет: Литература,
автор: Ukrne