Question

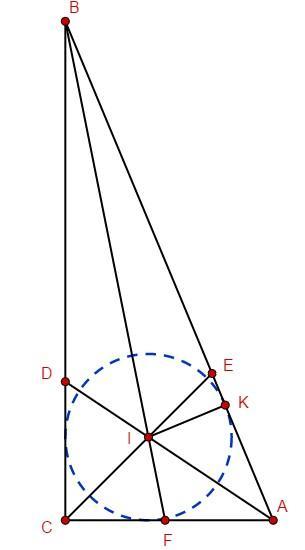
В треугольнике ABC угол C прямой. Известно, что BC=12, CA=5. Пусть I— точка пересечения биссектрис. Найдите расстояние от I до AB

Answer 1

Точка пересечения биссектрис является центром вписанной окружности, расстояние от точки $\sf I$ до $\sf AB$ это есть радиус вписанной окружности.

Найдем гипотенузу прямоугольного треугольника, по т. Пифагора

$\sf AB=\sqrt{12^2+5^2}=13$

Искомое расстояние: $\sf IK=\dfrac{a+b-c}{2}=\dfrac{12+5-13}{2}=2$

Ответ: 2.