Question

Решите пж ( с рисунком и подробно)даю много баллов

Answer 1

Ответ:

Объяснение:

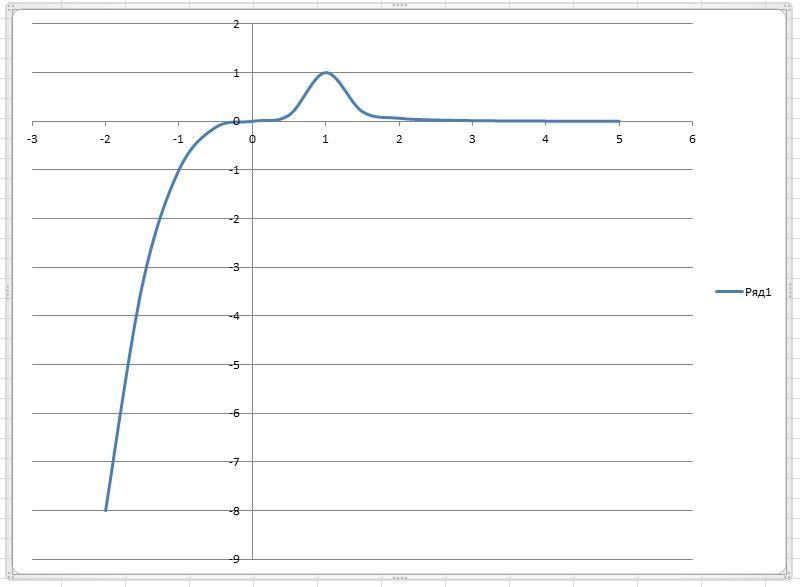
1)

$f(x)=x^{10}\\x^{10}'=10x^9\\10x^9=0=>x=0\\f(0)=0$

f(-1)=1; f(1)=1

Минимальное значение - 0 в точке (0;0)

Максимальное 1 в точках (-1;1) и (1;1)

2) график на рисунке

x²=y+4

точка минимума - (0;-4)

порабола имеет ветви вверх

y=∛х

y(0)=0 - функция возрастает.

У данных функций может быть 0, 1 или 2 точки пересечения. У данных функций есть две точки пересечения, так как точка экстремума пораболы лежит ниже точки экстремума корня

4)

$\frac{x}{f(x)} \leq 25x^{-1}f(\frac{1}{x}) , f(x)=x^{-3}\\\frac{x}{x^{-3}} \leq 25x^{-1}\frac{1}{x^{-3}}\\x^4\leq 25x^2\\x_1=\sqrt{5} , x_2=-\sqrt{5} \\x=0=>0\leq 0\\x=-3=>81> 225\\x=3=>81> 225\\\\f(x) - [-\sqrt{5} ;\sqrt{5}]$

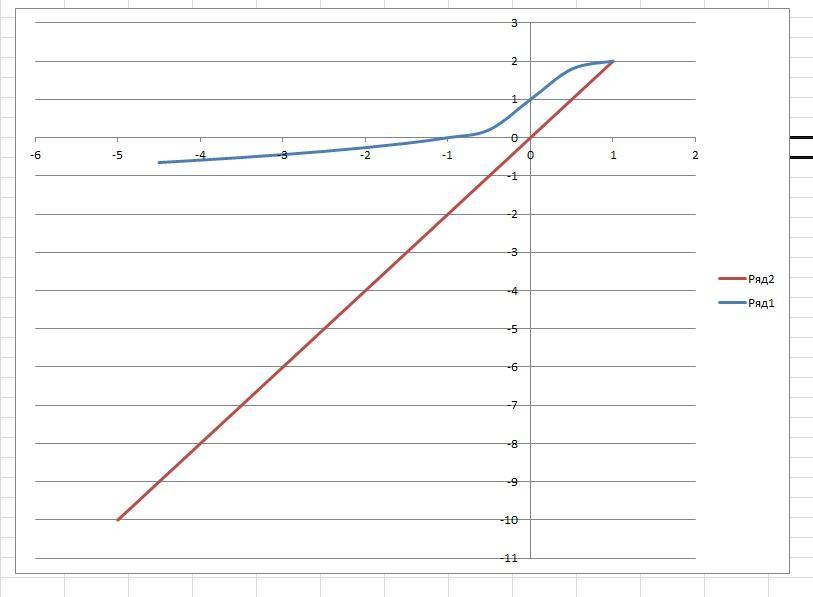
5) второй рисунок

решением будет 2x<y<∛x+1