Question

СРОЧНО ПОМОГИТЕ РЕШИТЬ

Answer 1

Ответ:

Пошаговое объяснение:

1)

$\int {(\frac{3}{9+x^2}+8x^7-x^4+5 )} \, dx =3\int {\frac{1}{9+x^2} } \, dx +\int {(8x^7-x^4+5 )} \, dx = \frac{3}{3} arctg\frac{x}{3} +x^8-\frac{1}{5} x^5+5x+C$

2)

$\int {(3x-3)sinx} \, dx =3\int {(x-1)sinx} \, dx=-3\int {(x-1)} \, dcosx=-3((x-1)cosx-\int {cosx} \, d(x-1)=(3-3x)cosx+3sinx+C$

3)

$\int\limits^1_0 {(5x-2)^4} \, dx =\frac{1}{5} \int\limits^1_0 {(5x-2)^4} \, d(5x-2) =\frac{1}{5} *\frac{(5x-2)^5}{5} |^1_0=\frac{1}{25} (243+32)=11$

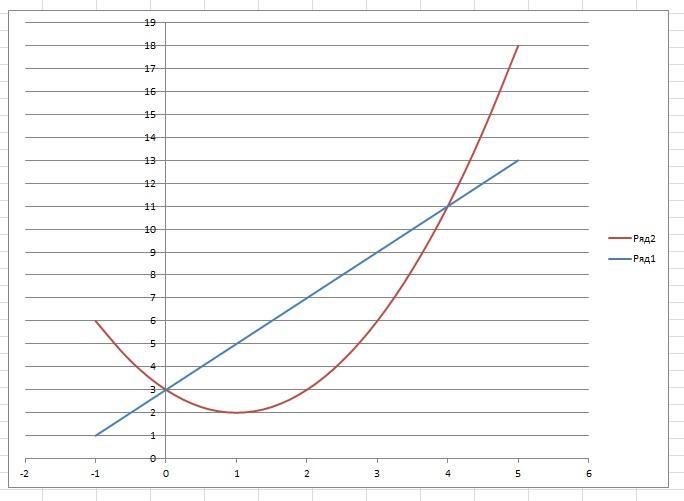
4) Фигура на рисунке

Площадь можно вычислить как разность площадей трапеции и площади фигуры ограниченной пораболой.

Площадь трапеции найдем по геометрической формуле:

S=(a+b)*h/2=(3+11)*4/2=14*2=28

Площадь второй фигуры равна:

$\int\limits^4_0 {(x^2-2x+3)} \, dx =(x^3/3-x^2+3x)|^4_0=64/3-16+12=21+1/3-4=17+1/3$

Искомая площадь равна: 28-17-1/3=10+2/3=32/3