Предмет: Алгебра,
автор: makarmaslenok
Задание 1.
Упростите выражение. Результат запишите в виде 1.png
2.png
Задание 2.
Упростите выражение. Найдите его значение при a = 48; b = 144.
3.png
Задание 3.
Упростите числовое выражение. Результат запишите в виде . Найдите его приближенное значение с помощью калькулятора.
4.png
Задание 4.
Сравните числа без использования калькулятора:
а) 6.pngи log2 20
б) 11120 и 5180
Задание 5.
На координатной плоскости схематически изобразите графики функций. Укажите их область определения и область значений.
а) y = (x + 1)2/3 - 5
б) 
Приложения:
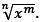
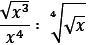
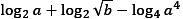
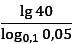
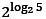
makarmaslenok:
Почему я увидел только 22.05 это сообщение, а не в марте?!
Ответы
Автор ответа:
15
Ответ:
Объяснение:
1)
2)a = 48; b = 144
3)
4)
a)
б) 111120>5180
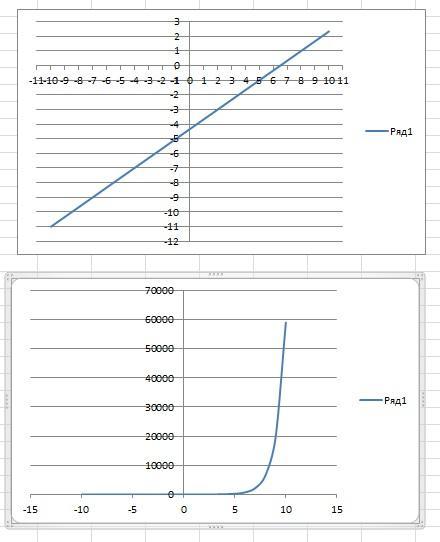
5)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: tima987
Предмет: Русский язык,
автор: mila2203
Предмет: Английский язык,
автор: пуняева
Предмет: История,
автор: vikaselezneva
Предмет: Информатика,
автор: artemfrik65