Question

В прямоугольной трапеции меньшая боковая сторона равна 6см и составляет
с меньшей диагональю угол 45°. Острый угол трапеции также равен 45°.
Найдите площадь трапеции.​

Answer 1

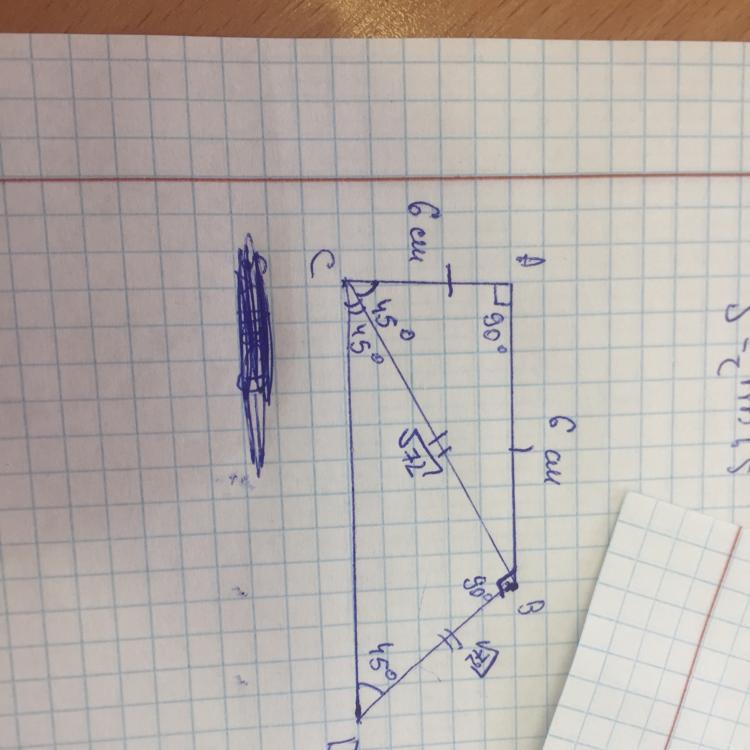
1. А, В, С, Д - вершины трапеции. АВ = 6 см - меньшая боковая сторона. АС - меньшая

диагональ. Угол ВАС = 45°. Угол Д = 45°.

2. Угол АСВ = 180° - 45° - 90° = 45°.Так как углы при основании АС равны, треугольник АВС

равнобедренный. АВ = ВС = 6 см.

3. Из вершины С проведём высоту ВН.

4. Угол ДСН = 180° - 45° - 90° = 45°. Треугольник СДН также равнобедренный. СН = ДН = 6

см.

5. АД = ДН + АН.

АН = ВС = 6 см.

АД = 6 + 6 = 12 см.

6. Площадь трапеции АВСД = (ВС + АД)/2 х СН = (6 + 12)/2 х 6 = 54 см^2.

Answer 2

Дано:
ABDC - трапеция
AC=6см
УголD=45 градусов
УголACB=45 градусов
Решение:
SтрABC=18 см2
SтрCBD=36 см2
SABDC=18+36=54 см2
Ответ: 54 см2