Предмет: Геометрия,
автор: sayateruzak2005
Диагональ равносторонней трапеции перпендикулярна боковой стенке. Найдите площадь трапеции, если большая подошва равна 8√3, а угол трапеции равен 60 °.
Помоги пожалуйста
Ответы
Автор ответа:
14
1) Ответ: 36√3 ед²
Объяснение:
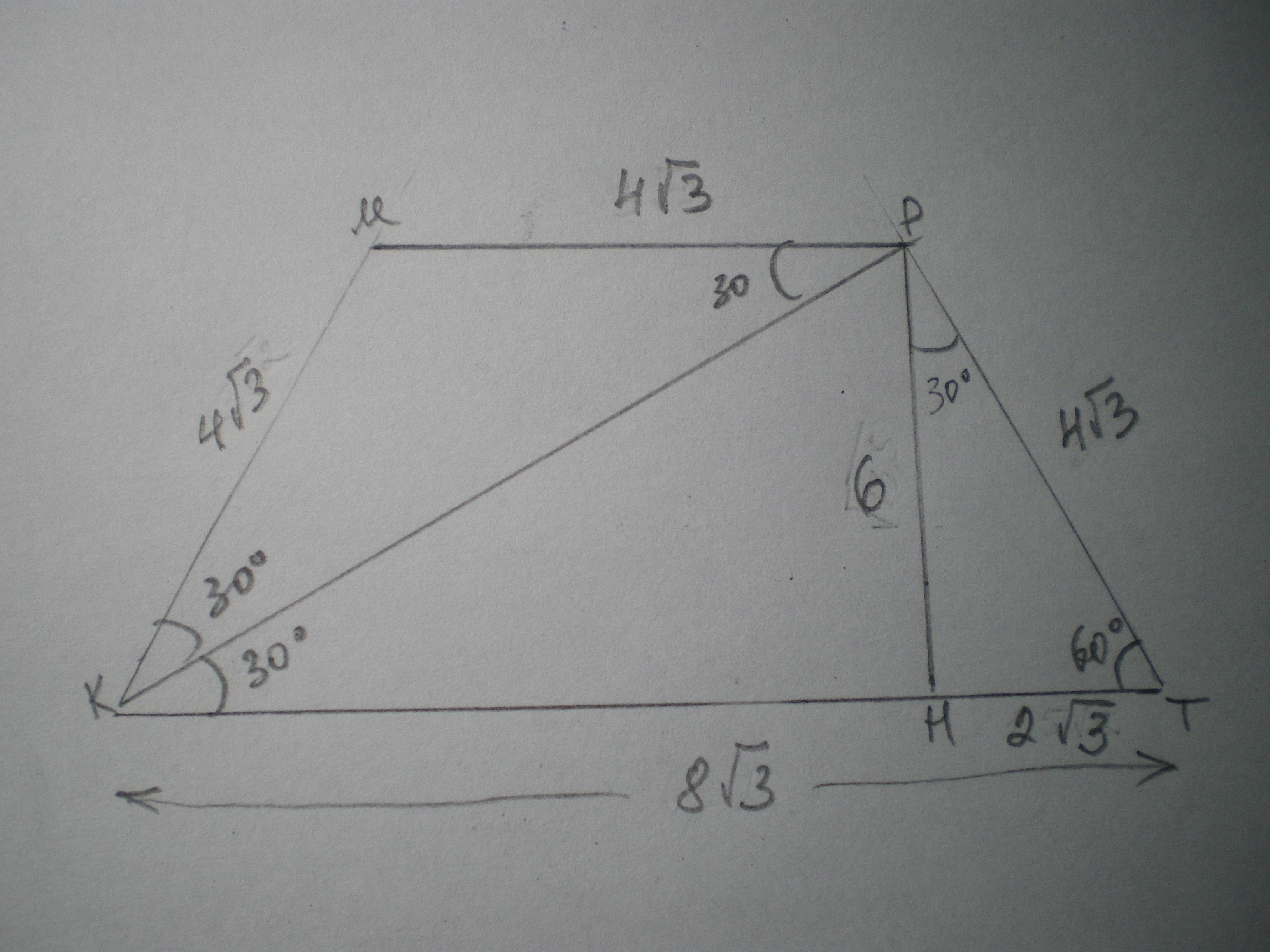
Дано: КМРТ - трапеция, КМ=РТ, ∠Т=60°, КР⊥РТ; КТ=8√3. Найти S(КМРТ).
Рассмотрим ΔКРТ - прямоугольный; ∠РКТ=90-60=30°, значит, РТ=0,5КТ=4√3 по свойству катета, лежащего против угла 30 градусов.
Проведем высоту РН и рассмотрим ΔРТН - прямоугольный;
∠ТРН=90-60=30°, значит, ТН=0,5РТ=2√3.
Найдем РН по теореме Пифагора:
РН²=РТ²-ТН²=48-12=36; РН=6.
Найдем МР. ∠МРК=∠РКН=30° как внутренние накрест лежащие при МР║КТ и секущей КР; ∠МКР=60-30=30°, значит, ΔКМР - равнобедренный, МР=КМ=4√3.
S(КМРТ)=(МР+КТ)/2 * РН = (8√3+4√3)/2 *6=(6√3)*6=36√3 ед²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Andrey66
Предмет: Английский язык,
автор: Adildag
Предмет: Русский язык,
автор: дану
Предмет: Алгебра,
автор: angeltonks
Предмет: География,
автор: wffwfwfw
данного вида линейным подпространством в R^3? Если да, то найти базис и размерность этого подпространства R^3 . Дополнить базис подпространства L = {(x1, x2 ,x3)} до базиса всего пространства.
а) ( 2а-2; -3а+2b; 2a+b)
б) ( 2a-2b; - 3a+2b; 2a+b)