Предмет: Алгебра,
автор: jpark3240
СРОЧНО!!!! ДАМ 30 БАЛЛОВ!!!
Приложения:
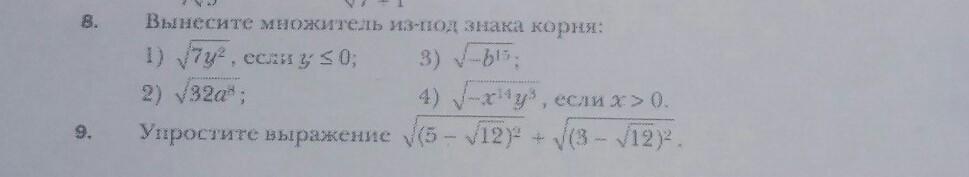
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Вика1998loveyou
Предмет: Русский язык,
автор: LOVE3738
Предмет: Русский язык,
автор: красава565259
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: lichevacaterin