Question

Из точки А к окружности с центром О проведены две касательные АВ и АС (В и С это точки касания). угол ВАС в 2 раза меньше угла ВОС. Периметр треугольника ВАС равен 14√3. Найдите радиус окружности.

Answer 1

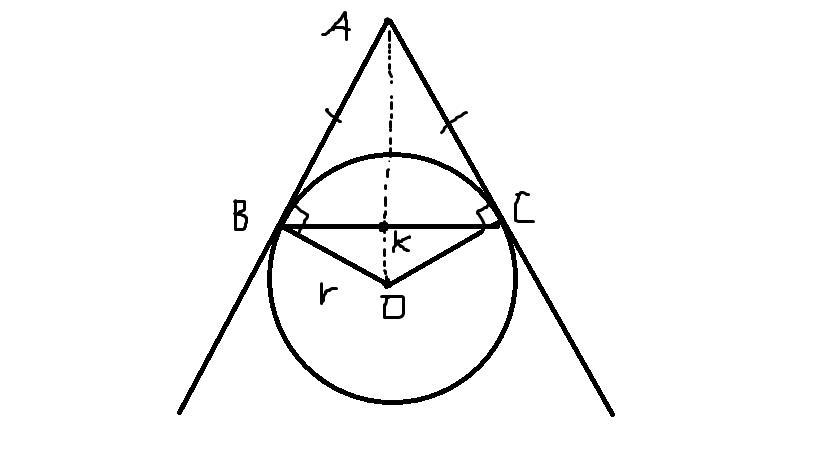
Чертеж приложен.

Проведем радиусы в точки касания. В образованном четырехугольнике ABOC имеем: ∠B = ∠C = 90° (радиус, проведенный в точку касания, перпендикулярен касательной);   ∠A = ∠O/2 ⇒ ∠О = 2∠А

Сумма углов четырех угольника равна 360°:

∠А + ∠В + ∠С + ∠О = 360°,

∠А + 90° + 90° + 2∠А = 360°,

3∠А = 180 ⇒ ∠А = 60° ⇒ ∠О = 120°.

По теореме об отрезках касательных, проведенных из одной точки, AB = AC, AO - биссектриса угла BAC. Обозначим точку К на отрезке АО, причем K  ∈ BC.

Так как ∠А = 60°, то данный треугольник - равносторонний (так как любой равнобедренный треугольник, у которого хотя бы один угол равен 60°, является равносторонним. Отсюда каждая сторона треугольника АВС равна $\frac{14\sqrt3}{3}$ (так как периметр будет равен утроенной стороне).

Тогда

$BK=BC/2=\frac{7\sqrt3}{3}$

Рассмотрим прямоугольный треугольник ВОК (∠К = 90°). ∠О = 60° (так как ОК - биссектриса треугольника ВОС и делит соответствующий угол пополам.

По определению синуса $BK/OB=\sin O$, откуда $OB = R = \frac{OK}{\sin O} = \frac{7\sqrt3}{3} : \sin 60\textdegree =\frac{7\sqrt3}{3}:\frac{\sqrt3}{2}=\frac{7\sqrt3}{3} \cdot\frac{2}{\sqrt3}=\frac{14}{3}$

ОТВЕТ: $4\frac{2}{3}$.