Question

Точка P удалена от всех вершин прямоугольного треугольника на расстояние 2a, а от его плоскости - на расстояние a. Найдите медиану треугольника, проведённую из вершины прямого угла? (можно пожалуйста с чертежом?())

Answer 1

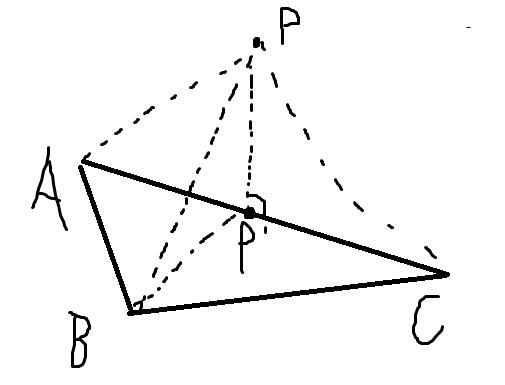
Чертеж приложен.

Пусть АВС - заданный треугольник, P' - проекция точки P на гипотенузу АС. Так как по условию точка P равноудалена от вершин треугольника, то и точка P' будет равноудалена от всех вершин треугольника - следовательно, P' - центр окружности, описанной около трегольника АВС.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы. Но так как медиана прямоугольного треугольника, проведенная из вершины прямого угла, также равна половине гипотенузы, то она равна все тому же радиусу описанной окружности, которую можно легко найти из треугольника APP', где ∠P' = 90°.

По теореме Пифагора $AP^2=AP'^2+PP'^2\Rightarrow AP'=\sqrt{AP^2-PP'^2}=\sqrt{(2a)^2-a^2}=\sqrt{4a^2-a^2}=\sqrt{3a^2}=a\sqrt3$

Итого искомая медиана равна $a\sqrt3$.

ОТВЕТ: $a\sqrt3$.