Question

ПОМОГИТЕ ПОООЖАААЛУЙСТА,МНЕ НУЖНО СРОЧНО
Равнобедренный прямоугольный треугольник с гипотенузой 112√ см вращается вокруг катета.
Определи радиус, высоту и объём конуса, который образовался (π≈3).

R= см;H= см;V= см3.

Answer 1

• Катеты равнобедренного, прямоугольного треугольника равны.

Пусть катет равен x см, тогда по теореме Пифагора:

x²+x² = (11√2)²;

2x² = 11²·2;

x² = 11²;

x = 11.

Катеты равны по 11 см.

• Если прямоугольный треугольник, с катетами a и b, вращать вокруг катета a, то получится конус с высотой a и радиусом основания b.

Откуда R = 11см; H = 11см.

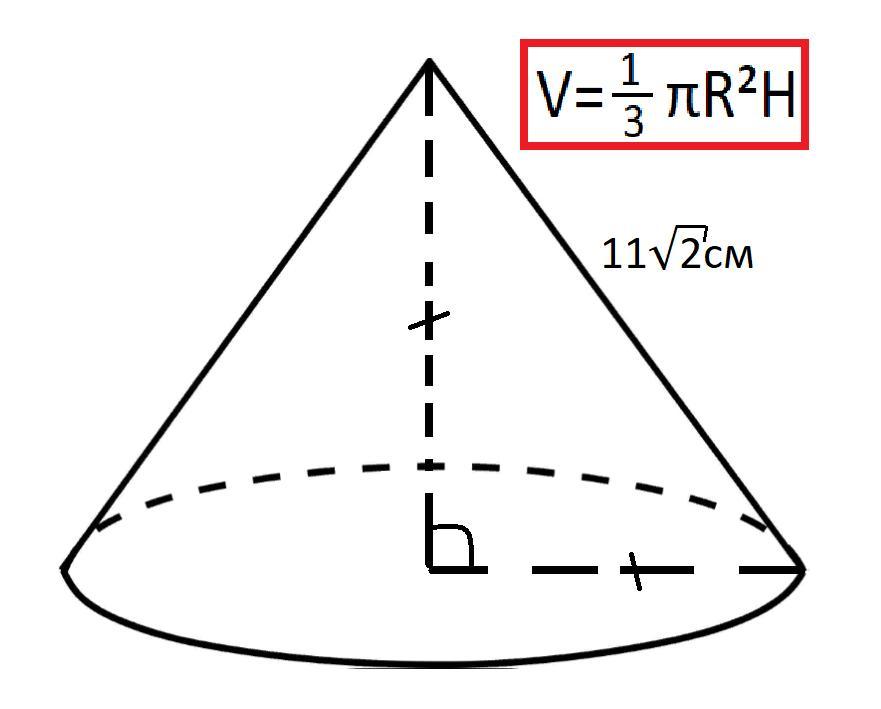
• Объём (V) конуса вычисляется по формуле: $V=\dfrac{1}{3}\cdot \pi\cdot R^2\cdot H$, где R - радиус основания, H - высота конуса, π - математическая постоянная.

V = (1/3)·π·(11см)²·11см;

V = (π/3)·11³ см²;

При π≈3:

V = (3/3)·1331 см³ = 1331 см³.

Ответ: R = 11см;  H = 11см;  V = 1331см³.